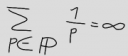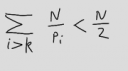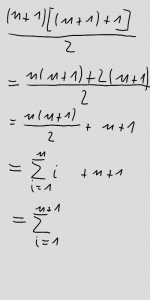kirjoittaessani

What would we do without referrers? I do not really know, but bloggers would have to do without a lot of funny search requests.

A few days ago, someon was looking for a Rechenregel wie man erkennt durch welche Zahlen eine Zahl teilbar ist. That roughly translates as rule how to recognize by which numbers a number is divisible. Anyway, I am happy to provide a few. All rules are equivalencies, that is the given number is divisible if the rule is fulfilled; otherwise, it is not divisible.

1. every number is divisible by one 🙂
2. the final digit is divisible by two
3. the cross total (sum of digits) is divisible by three
4. the number comprised of the final two digits is divisible by four
5. the final digit is zero or five
6. both rules 2 and 3 hold
7. double the final digit and subtract it from the rest of the number; the result is divisible by seven; e.g. 203: 20-2*3=14 is divisible
8. the number comprised of the final three digits is divisible by eight
9. the cross total is divisible by nine
10. the final digit is zero
11. the alternating sum of digits is divisible by eleven, e.g. 135795: 1-3+5-7+9-5=0 is divisible
12. rules 3 and 4 hold
13. quadruple the final digit and add it to rest of the number; the result is divisible by thirteen; e.g. 403: 40+4*3=52; it is useful to apply the rule again: 5+4*2=13 isdivisible, so 52 is, and therefore 403 as well.

Well, that should suffice for now.

Mathematisches hat es hier ja schon länger nicht mehr gegeben; weil es schon spät ist, gibt es heute aber nur einen kurzen Beitrag.

Wenn wir n Objekte irgendwie auf r Schubladen verteilen, und r < n ist, dann landen in (mindestens) einer Schublade (mindestens) zwei Objekte. Das dürfte auch mathematisch wenig versierten Menschen unmittelbar einleuchten; die Mathematiker nennen diese Erkenntnis Schubfachprinzip, und man kann damit tatsächlich Beweise führen.

Zum Beispiel den:
Wenn wir zu irgendeinem n aus den Zahlen 1,2,3,…,2n irgendwie n+1 auswählen, dann gibt es darunter immer zwei, die teilerfremd sind.
Warum ist das so? Nun, zwei der n+1 Zahlen müssen aufeinanderfolgend sein, und aufeinanderfolgende Zahlen sind teilerfremd.

Das sieht man also noch recht einfach, aber wie wäre es damit:
Unter den gewählten n+1 Zahlen gibt es auch zwei, von denen eine ein Vielfaches der anderen ist.
Das sieht nicht so einfach aus, ist aber doch schnell zu zeigen: wir schreiben jede der n+1 Zahlen als a=2^km. Dabei soll m ungerade sein. Wie viele ungerade Zahlen gibt es zwischen 1 und 2n? Offenbar genau n. Also muß es — nach dem Schubfachprinzip — unter unseren n+1 Zahlen mindestens zwei geben, die sich das gleiche m teilen; sie unterscheiden sich demnach nur in k und damit in der Zahl der Zweien, die an das ungerade m multipliziert werden.
Dann ist aber die eine ein Vielfaches der anderen.

Und spät genug ist es jetzt auch.

…das war vor einiger Zeit recht beliebt bei den Suchanfragen, die hierher führen. Im Moment steht 1000 als summe aufeinanderfolgender zahlen hoch im Kurs.

Also gut: einmal Schummeln für unfähige Anfänger. Ihr dürft jetzt alle hier abschreiben und Euch dann wundern, wenn Ihr die nächste Klausur verhaut.

Summa cum

Wir wollen also schreiben können k+(k+1)+…+l = 1000.
Vom ollen Gauß wissen wir ja, daß die Summe der Zahlen von 1 bis n gegeben ist als n(n+1)/2. Wie sieht das also aus, wenn wir von k+1 bis l summieren? Ganz einfach: wir rechnen erstmal von Eins bis l, ziehen dann aber die zu kleinen Zahlen wieder ab. Also:

1000 = l(l+1)/2 - k(k+1)/2.

Anders formuliert könnten wir auch l=k+n setzen und sagen, daß wir n aufeinanderfolgende Zahlen ab k +1 summieren wollen. Dann haben wir:

1000 = (k+n)·(k+n+1)/2 - k(k+1)/2

Multiplizieren wir das ganze mit 2 und vereinfachen ein bißchen, dann haben wir diese schöne Formel:

2000 = n(2k+n+1)

Gerade oder ungerade, das ist hier die Frage

Das bedeutet: um 1000 als Summe aufeinanderfolgender Zahlen schreiben zu können, müssen wir 2000 als Produkt zweier Zahlen, nämlich n und 2k+n+1schreiben. Dabei kann n gerade oder ungerade sein; da 2k+1 aber immer ungerade ist, wird 2k+n+1 genau dann gerade sein, wenn n ungerade ist.
Jetzt zerlegen wir 2000 in seine Primfaktoren und überlegen, auf wie viele Arten wir daraus einen geraden und einen ungeraden Faktor basteln können. 2000=2⁴·5³; die Faktoren 2 müssen immer zusammen vorkommen, sonst wären ja beide Teile gerade, die anderen können wir verteilen:

2000 = 16·125 = 80·25 = 400·5 = 2000·1

Das war's auch schon, mehr als diese Varianten gibt es nicht. Jetzt müssen wir nur noch feststellen, ob jedem Produkt auch eine Darstellung der Zahl 1000 entspricht, und wie diese jeweils aussieht.

Aufgezählt

Die Zahl der Summanden, die in der Formel mit n angegeben ist, kann also höchstens die Werte 1, 5, 16, 25, 80, 125, 400, 2000 annehmen. Die probieren wir jetzt der Reihe nach durch:
Ist n=1, dann folgt 2k+n+1=2000, also k=999. Das ist das, was die Mathematiker gerne als triviale Lösung bezeichnen: eine Möglichkeit, 1000 als Summe aufeinanderfolgender Zahlen zu schreiben, ist die einzige Zahl 1000 — eine Folge aus einer Zahl.

n=5 ist schon interessanter: 2k+n+1=400, also k=197, das heißt die Summe hat fünf Glieder und startet oberhalb von 197: 1000=198+199+200+201+202.

n=16 liefert 2k+n+1=125, also k=54. Damit ist 1000 = 55+56+…+69+70.

Aus n=25 folgt 2k+n+1=80 und k=27: 1000 = 28+29+…+52.

Dann haben wir noch n=80, also 2k+n+1=125, k=22: 1000 = 23+24+…+102.

Bei n=125 ist dann Schluß: dann wäre 2k+n+1=80, und diese Gleichung läßt sich durch kein positives k mehr erfüllen.

Zum Schluß

Auf eine Sache sollte ich noch eingehen: warum dürfen wir hier eigentlich ganz munter räsonieren und Teiler aufschreiben, nur um hinterher zu sagen: ätsch, 125 (und die größeren) waren nur ein Scherz? Wäre es nicht genauso möglich, daß unsere Methode nicht nur blinde Passagiere wie die 125 ausspuckt, sondern auch richtige Lösungen (meinetwegen n=17) verschluckt?

Nein, das geht zum Glück nicht: mathematische Argumente sind, wenn sie sauber verwendet werden, exakt. Daß wir trotzdem zunächst einige Zahlen bekommen haben, die wir dann doch wieder verwerfen mußten, liegt an dem Unterschied zwischen einer Folgerung und einer Äquivalenz: Wenn 1000 sich als die Summe der Zahlen k+1 bis k+n schreiben läßt, dann gelten die oben gemachten Überlegungen, und dann muß schließlich n ein Teiler von 2000 sein. Das heißt aber nicht, daß sich umgekehrt auch jede Zahl n, die Teiler von 2000 ist, automatisch in eine solche Summe verwandeln läßt. Dazu muß noch mehr gelten, n darf nämlich nicht nur irgendein Teiler von 2000 sein, sondern muß gerade komplementär zu 2k+n+1 sein. Wenn das nicht erfüllbar ist (z.B. für n=125), dann fallen die restlichen Überlegungen flach.

So, jetzt ist aber genug geschummelt.

[Edit: diverse Typos]

Referrer sind doch eine tolle Sache — so bekommt man erst mit, was die Be-sucher denn so alles suchen. Einer wollte neulich alle primzahlen aufgezählt haben.
Damit kann ich leider nicht dienen, denn es gibt eine ganze Menge Primzahlen — unendlich viele, um genau zu sein.

Viel

Geht es noch genauer? Unendlich ist ja nicht gleich unendlich. Nimmt man zum Beispiel nur die geraden Zahlen (2, 4, 6, 8, 10, …), so gibt es davon offenbar[1] weniger als von den natürlichen Zahlen (1, 2, 3, 4, …). Von den "runden" Zahlen (1, 10, 100, 1000, …) gibt es dann noch weniger. Wie mag es wohl mit den Primzahlen aussehen?
Es gibt so viele Primzahlen, daß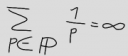

Häh?

OK, der Reihe nach; zuerst stellt sich die Frage, was da eigentlich steht. Das ist relativ einfach. Wenn wir alle Primzahlen nehmen (pϵP), zu jeder den Kehrwert bilden (1/p), und diese Kehrwerte dann aufsummieren (Ʃ), dann wird das Ergebnis unendlich groß. Auf den ersten Blick ist das vielleicht nicht verwunderlich; immerhin addieren wir unendlich viele Zahlen, die alle positiv sind.
Wenn wir aber statt 1/p die reziproken Zweierpotenzen addieren, dann ist das Ergebnis durchaus endlich: 1/2+1/4+1/8+…=1. Warum? Naja, 1/2 ist die Hälfte von 1; 1/4 ist die Hälfte von dem, was dann noch zu 1 fehlt, und so weiter:

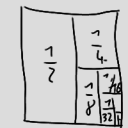
Wenn die Zahlen, deren Kehrwerte ich addiere, also schnell genug größer werden, dann kann die Reihe[3] konvergieren, also eine endliche Zahl als Ergebnis haben. Daß die Reihe der reziproken Primzahlen divergiert, bedeutet also, daß sie nicht sehr schnell größer werden — daß es also recht viele von ihnen gibt.

Langsam

Was heißt nicht sehr schnell? Nun, die Reihe der reziproken natürlichen Zahlen, 1+1/2+1/3+1/4+…, divergiert, i.e. die natürlichen Zahlen wachsen in diesem Sinne langsam. Die Quadratzahlen wachsen dagegen schnell, 1+1/4+1/9+1/16+… konvergiert nämlich[4] — nimmt man stattdessen dritte oder vierte Potenzen, so wachsen die Zahlen natürlich schneller, und die Reihen konvergieren auch. Man kann zeigen, daß Ʃ1/n^r immer konvergiert, solange r nur größer als 1 ist. Es reicht, r=1,001 (oder noch kleiner) zu wählen. Das heißt, daß die Folge der Primzahlen tatsächlich sehr langsam wachsen muß, damit die Reihe divergiert.

An's Eingemachte

Behaupten kann man viel, wenn der Tag lang ist. Mathematiker wollen aber immer Beweise dafür sehen. Der, den ich hier vorführen möchte, stammt von dem berühmten Ungarn Erdős. Ich folge dabei dem Buch von Aigner und Ziegler[5].

Der Beweis ist wieder ein Widerspruchsbeweis, i.e. wir nehmen an, daß die Behauptung gerade nicht stimmt, rechnen ein bißchen herum und finden dabei einen Widerspruch. Daraus folgt dann, daß die Annahme falsch war.

Nehmen wir also an, daß die Reihe konvergiert. Wenn wir nun die ersten Summanden überspringen, dann wird die Gesamtsumme kleiner, und wenn wir genügend Summanden überspringen, können wir die Gesamtsumme kleiner als 1/2 machen.[6]

Wählen wir also k genügend groß, und denken wir uns noch irgendeine Zahl N aus, mit der wir die ganze Ungleichung multiplizieren, dann gilt:

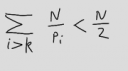
Wenn wir jetzt alle Zahlen betrachten, die nicht größer sind als N, dann gibt es solche, die sich durch eine Primzahl teilen lassen, die in unserer verkürzten Reihe vorhanden ist; ihre Anzahl wollen wir b nennen. Und es gibt solche, die nur Primteiler besitzen, die unter den ersten k Primzahlen sind und deswegen nicht in der verkürzten Reihe vorkommen; ihre Anzahl sei s. Weil alle Zahlen entweder zu der einen oder anderen Kategorie gehören müssen, ist s+b=N.

Wie groß ist b? Nun, für eine Primzahl p_i gibt es Zahlen, die durch sie teilbar sind. Wenn wir diesen Ausdruck über alle Primzahlen summieren, dann liegen wir vielleicht zu hoch, aber sicher nicht zu niedrig[7].
Wenn wir also summieren, dann steht wieder unsere Ungleichung von oben da, und es gilt: b < N/2.

Wie sieht es für s aus? Das geht anders, und zwar so: Wir schreiben jede Zahl n, die zu s zählt, als n=a·q². Dabei ist a das Produkt aller Primfaktoren, die in n nur einmal vorkommen. Zum Beispiel ist 150=2·3·5·5, also a=2·3=6 und q=5.
Um die Frage zu klären, wie groß s ist, müssen wir also überlegen, wie viele verschiedene a und q es gibt. Das ist einfach: in a kommt jede Primzahl einmal oder keinmal vor, das sind zwei Möglichkeiten pro Primzahl. Da für s nur die ersten k Primzahlen in Frage kommen, sind das 2·2·2…=2^k Möglichkeiten. Bei q machen wir es uns ganz einfach: q² ≤ n, und n ≤ N, also q ≤ √N.

Damit ist s ≤ 2^k√N.

Widerworte

Am Anfang hatten wir uns ja ein N ausgedacht, aber alle Überlegungen waren völlig allgemein. Wir können uns jetzt also noch umentscheiden und zum Beispiel N=2^2k+2 nehmen. Dann ist s ≤ s^2k+1 (Einsetzen in die letzte Gleichung vom vorigen Absatz), also kleiner als N/2.

Weil b aber auch kleiner als N/2 ist, muß s+b kleiner als N sein.
Am Anfang hatten wir aber gesehen, daß s+b gerade gleich N ist. Beides gleichzeitig geht nicht, und da haben wir unseren Widerspruch.

Ende

Also, lieber unbekannter Google-User: es gibt nicht nur unendlich viele, sondern sogar verdammt viele Primzahlen, und die kann ich Dir unmöglich alle aufzählen.

Noten

[1] Ganz so einfach ist die Sache eigentlich nicht, dann auf eine sehr intuitive[2] Art gibt es gleich viele gerade und natürliche Zahlen. Das hört sich jetzt seltsam an, weil ja jede gerade Zahl eine natürliche ist, es aber auch natürliche Zahlen gibt, die nicht gerade sind — die ungeraden eben. Man kann aber von unendlichen Mengen durchaus einige Elemente wegnehmen, ohne daß die Menge kleiner würde.
In der Tat läßt sich diese Eigenschaft als Definition von unendlich verwenden.

[2] Vielleicht schreibe ich dazu noch einen Eintrag.

[3] Eine Reihe ist, vereinfacht gesagt, eine Summe unendlich vieler Zahlen.

[4] Und zwar gegen π²/6.

[5] Dieses Buch, das in Anlehnung an eine Idee von Erdős Das BUCH der Beweise heißt, kann man gar nicht genug loben. Deswegen wandert es jetzt erstmal in meine Sidebar.

[6] Das ist eine Eigenschaft von Grenzwerten. Letztlich ist der Grund der, daß die Reihe sich an ihr Ergebnis heranschleicht.

[7] Zu hoch deshalb, weil wir einiges doppelt zählen: 6 ist zum Beispiel durch 2 und 3 teilbar, und wir würden sie einmal bei den Vielfachen von 2, einmal bei denen von 3 zählen.

Es wird Zeit, sich noch einmal mit Landkarten zu beschäftigen. Wir haben bereits gesehen, daß ein Tuschekasten für Kartographen mindestens vier Farben enthalten muß. Außerdem braucht man dann, wenn für jedes Land eine Liste von Farben gebildet werden soll, höchstens mehr, niemals aber weniger Farben.
Noch offen ist aber die Frage, ob ich einen Tuschekasten zusammenstellen kann, mit dem jeder Kartograph für alle Karten auskommt.

Behauptung

Ich behaupte: ja, das geht. Fünf Farben reichen aus.
Mehr noch: es genügt sogar, wenn für jedes Land eine Liste mit fünf Farben zur Verfügung steht. (Wir hatten ja gesehen, daß das ein schwierigeres Problem ist.)

Induziert

Wie beweist man das am besten? Das Verfahren der vollständigen Induktion bietet sich hier an: Eine Karte mit nicht mehr als fünf Ländern kann ich natürlich immer mit fünf Farben zeichnen (Induktionsanfang). Wenn ich jetzt aus einer Karte mit n Ländern auf geschickte Weise ein Land eliminieren könnte, wäre ich schon am Ziel. Aber wie stellt man das an?
Als erstes greifen wir tief in die Trickkiste und fördern etwas zutage, das sich Warum einfach, wenn's auch kompliziert geht? nennt: wir beweisen schlichtweg etwas, das schwieriger (stärker) ist, und machen uns die Arbeit dadurch einfacher. Das hört sich seltsam an; der Grund liegt aber darin, daß wir uns sozusagen auf der Leiter von Sprosse zu Sprosse hangeln. Wenn wir alle Sprossen etwas höher einbauen, müssen wir zwar mit jedem Schritt etwas höher hinauf als bei unserer Originalleiter, aber wir starten ja auch jeden Schritt von einer höheren Sprosse aus.

Wirklich schwieriger wird nur die erste Sprosse; die ist aber bei Induktionsbeweisen kein wirkliches Problem. Zugegeben, ein bißchen hinkt die Analogie schon: wenn ich die Behauptung stärker mache, so kann der Beweis tatsächlich gleich schwer bleiben (wie bei der Leiter), er kann aber auch schwieriger oder einfacher werden. Hier wird er erfreulicherweise einfacher.

Weiter im Text

Weiter wollen wir annehmen, daß es höchstens Drei-Länder-Ecke gibt — aber keine Vier-, Fünf-, oder Noch-mehr-Länder-Ecke.

Wenn wir es doch einmal mit einer solchen Karte zu tun haben sollten, wollen wir einfach die Grenzen ein bißchen verschieben. Das ist nicht schlimm, weil das Problem dadurch nur schwieriger wird, die neue Lösung also auf jeden Fall auch Lösung des ursprünglichen Problems ist.

Behaupten kann man viel

Sehen wir uns eine Karte an, dann gibt es dort immer einen Ring von äußeren Ländern; hier sind es z.B. Washington, Oregon, Kalifornien, Arizona, New Mexico, Texas und so weiter.

Seien nun zwei benachbarte Länder dieses Rings bereits eingefärbt; jedes weitere Land auf dem Ring stelle eine Liste mit (mindestens) drei Farben bereit; jedes Land aus dem Inneren stelle eine Liste mit mindestens fünf Farben bereit.
Dann — so unsere Behauptung — können wir die gesamte Karte unter Benutzung dieser Listen einfärben.

Stärke

Diese Behauptung hat mit unserem ursprünglichen Ziel — der Einfärbung der Karte unter Benutzung von Fünfer-Farblisten — nicht mehr viel zu tun. Sie ist aber stärker: Wir behaupten jetzt, daß nur die inneren Länder noch Fünfer-Listen bereitstellen sollen; die Länder auf dem Ring liefern nur noch Dreier-Listen, zwei geben ihre Farbe sogar fest vor. Wenn wir die Karte unter diesen Bedingungen färben können, kommen wir mit Fünfer-Listen auf jeden Fall hin.

Aller Anfang ist leicht

Wenn nur drei Länder auf der Karte sind, so reichen uns die Farben auf jeden Fall: zweie sind ja schon gefärbt, und das dritte bietet uns eine Liste mit drei Farben an; egal, welche Farben durch die beiden Nachbarn belegt sind, eine bleibt immer frei.

Ein kleiner Schritt für einen Kartographen

Erinnern wir uns an die Vorgehensweise beim Induktionsschritt: wir müssen die Behauptung für eine Karte mit n Ländern beweisen, dürfen aber annehmen, sie sei für n-1 Länder, ja sogar für alle möglichen Karten mit weniger als n Ländern bereits bewiesen. Wir müssen also unsere große Karte auf eine (oder zwei) kleinere Karten zurückführen.
Nehmen wir nun an, zwei Länder aus dem äußeren Ring haben eine gemeinsame Grenze, die aber selbst nicht nach außen stößt; der Ring hat dann die Form einer Acht. Zaire und der Sudan sind ein Beispiel.

Jetzt können wir die Karte in zwei Teile zerlegen: die eine enthält Zaire, den Sudan, und alle weiter nördlich gelegenen Länder; die andere enthält ebenfalls Zaire und den Sudan, dazu aber die südlicheren Länder. Für Zaire und den Sudan vergeben wir jetzt je eine Farbe fest (etwa grün und rot); alle anderen Länder auf dem alten Ring haben Listen mit drei Farben, die inneren Länder deren fünf — so war ja die Voraussetzung. Dann gilt das aber auch für jede der beiden neuen "halben" Karten. Da diese kleiner sind, dürfen wir die Behauptung als bereits bewiesen ansehen. Beide kleinen Karten sind also mit den vorgegebenen Farben einfärbbar, und damit auch die gesamte Karte.
Das war es auch schon — mehr hatten wir gar nicht behauptet.

Unachtsam

Was nun, wenn der äußere Ring nicht die Form einer Acht hat?
Dann müssen wir die Zahl der Länder eben auf andere Art verringern. Nehmen wir die Karte der USA von oben, dann hat der äußere Ring dort nicht die Form einer Acht.

Angenommen, Washington sei bereits blau gefärbt. Auf dem Ring hat dieser Staat zwei Nachbarn: Idaho und Kalifornien. Angenommen, Idaho sei ebenfalls gefärbt (nach Annahme muß es ein Nachbar Washingtons auf dem Ring sein; es bleiben also nur CA oder ID). Dann entfernen wir jetzt probehalber Kalifornien von der Karte. Dadurch wird Nevada neu in den äußeren Ring aufgenommen — bei einer anderen Karte könnte natürlich auch eine ganze Reihe von Staaten dazukommen.
Nach Annahme hat Kalifornien (mindestens) eine Liste von drei Farben zur Verfügung gestellt; davon müssen mindestens zwei von Blau verschieden sein (sagen wir, Rot und Gelb). Diese beiden Farben streichen wir jetzt von der Farbliste Nevadas. Da die Liste vorher mindestens fünf Farben enthielt, bleiben also jetzt noch drei. Das heißt aber, daß die neue Karte (ohne Kalifornien) alle Voraussetzungen erfüllt, um vorschriftsmäßig gefärbt zu werden. Wenn wir jetzt noch eine Farbe für Kalifornien finden, sind wir fertig. Das ist aber leicht:
Nevada kann weder rot noch gelb sein, da wir diese Farben von der Liste gestrichen haben. Washington ist schon blau, und Arizona kann entweder Rot oder Gelb (oder eine andere Farbe) erhalten, aber nicht beide; deswegen bleibt eine der beiden Farben Rot und Gelb für Kalifornien.

Das war's, die Karte ist gefärbt!

Und sonst?

Im Falle der Farblisten ist Fünf tatsächlich die kleinste Zahl, die man finden kann. Margit Voigt hat ein Beispiel gefunden für eine Karte, die sich mit Vierer-Farblisten nicht immer einfärben läßt. Sie hat 238 Länder eingezeichnet.

Wenn es nur um den Tuschekasten geht, reichen dagegen sogar vier Farben. Der Beweis dafür ist allerdings leider viel zu lang und kompliziert für dieses Blog.

Der obige Beweis folgt übrigens dem Buch von Martin Aigner und Günther Ziegler, in dem sich — etwa auf Vordiplomniveau — eine ganze Reihe schöner Beweise findet.

Der Spiegel berichtet — nicht zum ersten Mal — über einen Bochumer Mathematiker, der die deutschen Zahlwörter ändern will: Einundzwanzig sei unlogisch, er möchte deshalb zwanzigeins einführen.
Der Artikel liest sich stellenweise, als ob der Untergang des Abendlandes oder doch wenigstens ein schlechtes Abschneiden bei der PISA-Studie drohte, wenn diese Änderung nicht durchgeführt wird. Ich habe da ein ganz anderes Problem: wo haben sie in dem Artikel nur die Smilies versteckt?

Beim letzten Mal haben wir gesehen, daß es Landkarten gibt, die mit weniger als vier Farben nicht gezeichnet werden können. Mit anderen Worten: wenn es eine Zahl n gibt, so daß mit n Farben beliebige Landkarten gezeichnet werden können, dann muß n≥4 sein.

Befindlichkeiten

Bevor wir nun untersuchen, ob wir auch eine obere Schranke für n finden können, wollen wir uns noch um einen anderen Aspekt kümmern: Wenn der kaiserliche Kartograph die Farben für die Karte aussucht, dann kann es vorkommen, daß die Landesfürsten mit den ihnen zugedachten Farben nicht zufrieden sind. Der eine hätte lieber Grün als Rot, dem anderen ist das Blau zu dunkel, und so weiter. Stattdessen die Fürsten ihre Farben aussuchen zu lassen, ist aber auch keine gute Idee: nachher müssen alle Länder in Gold dargestellt werden, und man erkennt überhaupt nichts mehr.
Deswegen hat sich der Kartograph folgende Regel ausgedacht: Jeder Landesfürst soll eine Liste mit k Farben, die ihm genehm sind, zusammenstellen. Die endgültige Auswahl der Farben aus diesen Listen nimmt der Kartograph dann selbst vor. Wie muß der Kartograph nun k wählen, damit er die Karte auf jeden Fall zeichnen kann? Wichtig ist dabei natürlich, daß k schon feststehen muß, bevor die Fürsten ihre Farben ausgesucht haben — unabhängig von deren Wahl muß die Karte machbar sein.

Mit und ohne Liste

Klar ist, daß k nicht kleiner als m sein kann, wenn für die vorliegende Karte mindestens m Farben benötigt werden; es wäre ja möglich, daß alle Fürsten zufällig die gleichen Listen abliefern — dann können nicht plötzlich weniger Farben als bei freier Farbwahl (für den Kartographen) nötig sein. Nun liegt der Verdacht nahe, daß k=m sein muß. Wenn alle Fürsten die gleiche Farbauswahl treffen, ist das naheliegend; anderenfalls kommen ja nur noch mehr Farben hinzu. Sechs Listen mit je zwei Farben enthalten zum Beispiel mindestens zwei Farben, es könnten aber auch mehr sein. Und wenn ich die Karte mit (beispielsweise) zwei Farben zeichnen kann, dann sollten sechs Listen mit je zwei Farben ja kein Problem sein. Wie gut, daß der Kartograph noch den kaiserlichen Mathematiker aufgesucht hat, bevor er die Boten zum Einsammeln der Farblisten ausschickte.

Weil unser Kartograph zu den Zeiten lebte, in denen noch gezaubert wurde, kann ich Euch leider keine echten Karten zeigen: sie sind alle durch die lange Zeit und die schädlichen Einflüsse der Zaubersprüche zerfallen. Stattdessen habe ich eine Karte von Obervolta, der Elfenbeinküste, Ghana, Togo, Benin und Atlantis ausgesucht. Na gut, Atlantis hat die Zaubersprüche auch nicht überstanden, da ist jetzt nur noch der Ozean. Das ändert aber an dem Problem nichts. Eine weitere Besonderheit von damals können wir heute nicht mehr sehen: die vier Länder in der Mitte hatten keine gemeinsamen Grenzen, weil die Zauberer für bodenlose Gräben zwischen ihnen gesorgt hatten. Deshalb können wir die Karte ganz einfach mit nur zwei Farben zeichnen:

Atlantis und Obervolta werden blau, die anderen vier Länder weiß.

Wie wir — und der kaiserliche Kartograph — oben angenommen haben, sollte es also ausreichen, wenn jeder Landesfürst zwei Farben zur Auswahl angibt. Was aber, wenn das Ergebnis so aussieht?

Obervolta will Rot oder Grün, Atlantis Gelb oder Blau, und so weiter. Jetzt haben wir ein Problem: Wir könnten Obervolta rot und Atlantis blau zeichnen, aber dann bleibt für die Elfenbeinküste keine Farbe übrig. Wenn Obervolta grün und Atlantis gelb wird, gibt es das gleiche Problem mit Benin. Die anderen beiden Kombinationen gehen auch nicht, weil dann entweder für Ghana oder Togo keine Farbe mehr bleibt.

Facit

Unsere Vermutung war also falsch: es gibt Karten, die sich mit m Farben vom Kartographen zeichnen lassen, nicht aber dann, wenn jeder Landesfürst eine Liste von m Farben zur Auswahl stellt, obwohl dann ja insgesamt mehr Farben zur Verfügung stehen. Umgekehrt ist aber jede Karte, die mit Farblisten zu je k Einträgen zu zeichnen ist, auch mit k Farben vom Kartographen zu zeichnen.

Auf politischen Landkarten verwendet man gerne Farben, um die einzelnen Staaten voneinander abzugrenzen. Wie viele verschiedene Farben man dafür braucht, hängt natürlich von der Karte, die man zeichnen möchte, ab.
Was aber, wenn ich einen Tuschekasten für Kartographen zusammenstellen möchte? Kann ich so viele Farben in den Kasten packen, daß meine Kunden damit auf jeden Fall auskommen — gleich, welche Karte sie zeichnen wollen?

Wenn zwei Länder schon dann unterschiedliche Farben erhalten sollen, wenn sie nur einen einzigen Punkt gemeinsam haben, dann ist die Antwort nein: im Reich des Tortenkaisers haben alle Königreiche einen Punkt gemeinsam, und deshalb brauchen die kaiserlichen Kartographen immer so viele Farben, wie es Könige gibt:

Wenn unterschiedliche Farben aber nur für solche Länder nötig sind, die tatsächlich ein Stück Grenze gemeinsam haben — vielleicht nur ein paar Meter — dann kann die Sache schon anders aussehen.

Wir haben jetzt zwei Aufgaben vor uns: zum einen wollen wir eine obere Schranke bestimmen, also eine Zahl von Farben, mit der wir auf jeden Fall auskommen; im Moment ist zwar nicht klar, ob so eine Zahl überhaupt existiert, aber davon lassen wir uns natürlich nicht aufhalten.
Zum anderen suchen wir auch eine Zahl von Farben, die (für zumindest eine denkbare Karte) zu klein ist. Diese Zahlen sollen natürlich so dicht wie möglich beieinander liegen, damit wir die kleinste Zahl von Farben, die auf jeden Fall ausreicht, gut eingrenzen können, und nicht übermäßig viele Farben in den Kasten packen.

Für heute soll der einfachere Teil genügen:

Untere Schranke

Um zu zeigen, daß n Farben zu wenig sind (und unser Tuschekasten also mindestens n+1 Farben enthalten muß), genügt es, eine Karte zu finden, die mit n Farben nicht mehr den Regeln entsprechend gezeichnet werden kann. Betrachten wir diese Karte von Luxemburg,

so stellen wir fest, daß wir hier vier Farben benötigen — jedes der vier abgebildeten Länder ist jedem anderen benachbart, und so braucht jedes auch seine eigene Farbe.

Einen Kasten mit nur drei Farben können wir also nicht verkaufen; festzustellen, ob es einen ausreichenden Kasten gibt, und wie groß dieser sein müßte, ist etwas schwieriger; deshalb hat das noch ein paar Tage Zeit.

Manchmal kommt es vor, daß man eine Reihe aufeinanderfolgender Zahlen addieren muß. Das ist zwar nicht schwierig, aber zeitraubend und recht eintönig. Zum Glück hat Gauß dafür eine Formel angegeben: Die Summe der ersten n natürlichen Zahlen ist gleich n(n+1)/2.
Der Legende nach ist Gauß als Schüler auf dieses Ergebnis gekommen, als er die Zahlen von Eins bis Hundert addieren sollte. Diese Rechnung dauert natürlich einige Zeit, aber seine Formel liefert ganz schnell 100·101/2=5050.

Wie kann man soetwas nun beweisen? Einfach nachrechnen funktioniert nur für gegebene Werte von n, zum Beispiel 1+2+3+4=10, 4·5/2=10 (stimmt!) — ein allgemeiner Beweis, daß die Formel für alle n gilt, ist das nicht.

Dafür haben sich die Mathematiker einen sehr nützlichen Trick einfallen lassen. Er funktioniert wie das Besteigen einer langen Leiter: auch wenn ich nicht genau weiß, wie viele Sprossen die Leiter hat, komme ich auf jeden Fall oben an, wenn ich zuerst vom Boden auf die unterste Sprosse und dann immer von einer Sprosse auf die nächste steige.

Also weisen wir zunächst die Gültigkeit der Formel für n=1 nach. Das ist nachgerade lächerlich einfach — die Summe der ersten einen natürlichen Zahl (was ein Satz) ist 1, und 1·2/2=1 ist auch klar.

Jetzt stehen wir also auf einer Sprosse und müssen auf die nächste klettern. Mit anderen Worten: wir müssen die Gültigkeit der Formel für die Zahl n+1 nachweisen unter der Voraussetzung, daß sie für n richtig ist. Wenn man das große Sigma(∑) als Zeichen für die Summe verwendet, dann sieht das so aus:

Man formt den Ausdruck etwas um und wendet zwischen der dritten und vierten Zeile die Formel für die Zahl n an — und das war es auch schon.

Diese Beweismethode nennt man vollständige Induktion (manchmal auch nur Induktion). Der meist sehr einfache Beweis für n=1 heißt Induktionsanfang, der Schritt von n auf n+1 Induktionsschluß oder Induktionsschritt. Außerdem gibt es noch die Induktionsannahme (auch Induktionsvoraussetzung), das ist die Annahme, daß die Formel für die Zahl n schon bewiesen sei.

Heute möchte ich mich mit einem Thema beschäftigen, das bei den meisten Menschen kein gutes Ansehen genießt: Mathematik. (Halt! Nicht wegklicken!)
Dabei soll es nicht um lustige Zahlenspielereien oder nützliche Rechenregeln gehen; vielmehr geht es mir um die Schönheit, die mathematische Aussagen und Beweise an den Tag legen, wenn man sie nicht als Mittel, sondern als Zweck betrachtet.
Die Idee dabei ist, einzelne Themen herauszugreifen und (hoffentlich) auch für Mathematik-Abstinenzler verständlich darzustellen.

Zu Anfang soll es um Primzahlen gehen. Die haben viele Vorteile: die meisten Menschen wissen, was Primzahlen sind; sie haben keine direkte Anwendung außerhalb der Mathematik (so daß man nicht so leicht abgelenkt wird); und man kann viele lustige Dinge mit ihnen anstellen.

Wenn der Mathematiker einen neuen Begriff einführt, dann tut er das mit einer Definition, die genau sagt, wie der Begriff zu verstehen ist. Primzahlen sind bekanntlich Zahlen, die nur durch Eins und sich selbst teilbar sind. Etwas genauer kann man definieren:
Eine natürliche Zahl n, deren Teilermenge genau zwei Elemente enthält, heißt Primzahl.
Daraus folgt, daß die Eins keine Primzahl ist, denn ihre Teilermenge enthält nur ein Element. Die umgangssprachliche Formulierung nur durch Eins und sich selbst teilbar ist da etwas unklar, was später zu Verwirrung führen könnte.

Welche konkreten Zahlen sind denn nun prim? Die ersten sind schnell aufgezählt: 2, 3, 5, 7, 11, 13, ...
Und wie geht es weiter? Vor allem: ist irgendwann Schluß, oder gibt es unendlich viele Primzahlen? Einerseits ist nicht recht einzusehen, warum es unendlich viele natürliche Zahlen, aber nur endlich viele Primzahlen geben soll; andererseits ist unsere Unfähigkeit, uns eine Welt mit endlich vielen Primzahlen vorzustellen, ein ziemlich schwaches Argument. Es muß also ein Beweis her. Vorher formulieren wir noch schnell einen Satz, der die zu beweisende Aussage formuliert:
Es gibt unendlich viele Primzahlen.
Eine häufig verwandte Methode ist die des Beweises durch Widerspruch: man nimmt einfach das Gegenteil der Behauptung an und leitet daraus einen Widerspruch her. Wenn die Schlußfolgerungen alle einwandfrei sein, muß die ursprüngliche Annahme falsch sein — und damit die Behauptung wahr.
Wir nehmen also an, es gäbe nur endlich viele Primzahlen, sagen wir n Stück. Diese numerieren wir durch: p₁, p₂, ..., p_n. Betrachten wir nun die Zahl x, die um eins größer als das Produkt aller Primzahlen ist: x=p₁p₂...p_n+1. Jede Zahl besitzt einen Primteiler, also auch x — das ist aber ein Widerspruch, denn p₁p₂...p_n ist ja per Konstruktion durch alle Primzahlen teilbar; zwei aufeinanderfolgende Zahlen haben aber keine gemeinsamen Teiler (außer 1).
[Das sieht man so: wenn n und n+1 beide durch p teilbar sind, dann gibt es x und y, so daß n=xp und n+1=yp, also xp+1=yp. Damit ist aber (y–x)p=1, also auch Eins durch p teilbar => Widerspruch, denn Eins besitzt (außer sich selbst) keine Teiler.]

Die Annahme, es gebe nur endlich viele Primzahlen, führt also auf einen Widerspruch, so daß es unendlich viele Primzahlen geben muß, q.e.d.