Wirklich witzige Google-Anfragen kann ich aus letzter Zeit leider nicht vermelden. Festzustellen bleibt lediglich, daß sich immer wieder Leute hierhin verirren, die auf ihre Fragen fast eine Antwort bekommen -- dann aber keinen Kommentar hinterlassen, sondern wortlos wieder abziehen. Wer nach povray mandelbulb sucht, will doch sicher den Code für das Fraktal in einer Form haben, die von PoV-Ray gelesen werden kann? Naja, vielleicht hilft es ja doch noch jemandem, wenn auch der ursprüngliche Besucher längst weg ist (siehe unten).
Außerdem: mein Hauptblog läßt sich wunderbar über Google finden; das Nibelungen-Projekt aber nur über die Blog-Suche. Das finde ich ein bißchen frustrierend, weil es für die Besucherzahlen alles andere als förderlich ist. Naja, vielleicht sollte ich trotzdem noch ein paar Seiten ablichten und vor allem auch transkribieren, damit die Suchmaschinen ein bißchen mehr Text zum Zerkauen haben.
So, das war's auch schon für heute. Ach ja, der Code:
#declare iteratex = function (x, y, z, a) {
a + pow(f_sphere(x,y,z,0),4)*sin(f_ph(y,z,x)*8)
*cos(f_th(y,z,x)*8)}
#declare iteratey = function(x, y, z, b) {
b + pow(f_sphere(x,y,z,0),4)*sin(f_ph(y,z,x)*8)
*sin(f_th(y,z,x)*8)}
#declare iteratez = function(x, y, z, c) {
c + pow(f_sphere(x,y,z,0),4)*cos(f_ph(y,z,x)*8)
}
isosurface {
function {
f_sphere(iteratex(iteratex(iteratex(x,y,z,x), iteratey(x,y,z,y), iteratez(x,y,z,z), x),
iteratey(iteratex(x,y,z,x), iteratey(x,y,z,y), iteratez(x,y,z,z), y),
iteratez(iteratex(x,y,z,x), iteratey(x,y,z,y), iteratez(x,y,z,z), z), x),
iteratey(iteratex(iteratex(x,y,z,x), iteratey(x,y,z,y), iteratez(x,y,z,z), x),
iteratey(iteratex(x,y,z,x), iteratey(x,y,z,y), iteratez(x,y,z,z), y),
iteratez(iteratex(x,y,z,x), iteratey(x,y,z,y), iteratez(x,y,z,z), z), y),
iteratez(iteratex(iteratex(x,y,z,x), iteratey(x,y,z,y), iteratez(x,y,z,z), x),
iteratey(iteratex(x,y,z,x), iteratey(x,y,z,y), iteratez(x,y,z,z), y),
iteratez(iteratex(x,y,z,x), iteratey(x,y,z,y), iteratez(x,y,z,z), z), z), 2)
}
}
[Edit: Typo in den Metadaten]
Kommentare deaktiviert für Gefindet
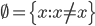 habe ich nicht zweimal hingesehen.
habe ich nicht zweimal hingesehen.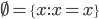 allerdings schon.
allerdings schon.





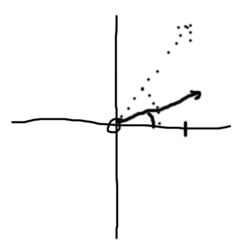 Wir denken unz zu jeder Zahl eine Art Uhrzeiger. Wenn wir die Zahl quadrieren wollen, dann quadrieren wir zuerst einfach seine Länge. Außerdem drehen wir den Zeiger ein Stück weiter: aus ein Uhr wird zwei Uhr, aus drei Uhr wird sechs Uhr, und aus vier Uhr wird acht Uhr. Bevor jetzt jemand fragt: bei den Mathematikern gehen die Uhren linksherum; und in diesem speziellen Fall fängt man auch gerne rechts statt oben an mit null Uhr.
Wir denken unz zu jeder Zahl eine Art Uhrzeiger. Wenn wir die Zahl quadrieren wollen, dann quadrieren wir zuerst einfach seine Länge. Außerdem drehen wir den Zeiger ein Stück weiter: aus ein Uhr wird zwei Uhr, aus drei Uhr wird sechs Uhr, und aus vier Uhr wird acht Uhr. Bevor jetzt jemand fragt: bei den Mathematikern gehen die Uhren linksherum; und in diesem speziellen Fall fängt man auch gerne rechts statt oben an mit null Uhr. Jetzt gehen wir nochmals zu den Folgen zurück und quadrieren munter drauflos. Das Ergebnis ist recht einleuchtend: unsere Zeigerzahlen drehen sich wild im Kreis, aber alle Zeiger länger als Eins wachsen ins unermeßliche, während die kürzeren ins Nichts schrumpfen.
Jetzt gehen wir nochmals zu den Folgen zurück und quadrieren munter drauflos. Das Ergebnis ist recht einleuchtend: unsere Zeigerzahlen drehen sich wild im Kreis, aber alle Zeiger länger als Eins wachsen ins unermeßliche, während die kürzeren ins Nichts schrumpfen.