JAN
2006
Manchmal kommt es vor, daß man eine Reihe aufeinanderfolgender Zahlen addieren muß. Das ist zwar nicht schwierig, aber zeitraubend und recht eintönig. Zum Glück hat Gauß dafür eine Formel angegeben: Die Summe der ersten n natürlichen Zahlen ist gleich n(n+1)/2.
Der Legende nach ist Gauß als Schüler auf dieses Ergebnis gekommen, als er die Zahlen von Eins bis Hundert addieren sollte. Diese Rechnung dauert natürlich einige Zeit, aber seine Formel liefert ganz schnell 100·101/2=5050.
Wie kann man soetwas nun beweisen? Einfach nachrechnen funktioniert nur für gegebene Werte von n, zum Beispiel 1+2+3+4=10, 4·5/2=10 (stimmt!) — ein allgemeiner Beweis, daß die Formel für alle n gilt, ist das nicht.
Dafür haben sich die Mathematiker einen sehr nützlichen Trick einfallen lassen. Er funktioniert wie das Besteigen einer langen Leiter: auch wenn ich nicht genau weiß, wie viele Sprossen die Leiter hat, komme ich auf jeden Fall oben an, wenn ich zuerst vom Boden auf die unterste Sprosse und dann immer von einer Sprosse auf die nächste steige.
Also weisen wir zunächst die Gültigkeit der Formel für n=1 nach. Das ist nachgerade lächerlich einfach — die Summe der ersten einen natürlichen Zahl (was ein Satz) ist 1, und 1·2/2=1 ist auch klar.
Jetzt stehen wir also auf einer Sprosse und müssen auf die nächste klettern. Mit anderen Worten: wir müssen die Gültigkeit der Formel für die Zahl n+1 nachweisen unter der Voraussetzung, daß sie für n richtig ist. Wenn man das große Sigma(∑) als Zeichen für die Summe verwendet, dann sieht das so aus:
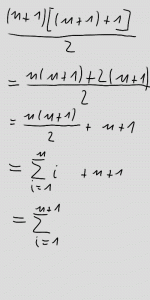
Man formt den Ausdruck etwas um und wendet zwischen der dritten und vierten Zeile die Formel für die Zahl n an — und das war es auch schon.
Diese Beweismethode nennt man vollständige Induktion (manchmal auch nur Induktion). Der meist sehr einfache Beweis für n=1 heißt Induktionsanfang, der Schritt von n auf n+1 Induktionsschluß oder Induktionsschritt. Außerdem gibt es noch die Induktionsannahme (auch Induktionsvoraussetzung), das ist die Annahme, daß die Formel für die Zahl n schon bewiesen sei.
0:24 Kommentare deaktiviert für Gaußvon kirjoittaessani