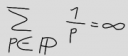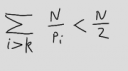Referrer sind doch eine tolle Sache — so bekommt man erst mit, was die Be-sucher denn so alles suchen. Einer wollte neulich alle primzahlen aufgezählt haben.
Damit kann ich leider nicht dienen, denn es gibt eine ganze Menge Primzahlen — unendlich viele, um genau zu sein.
Viel
Geht es noch genauer? Unendlich ist ja nicht gleich unendlich. Nimmt man zum Beispiel nur die geraden Zahlen (2, 4, 6, 8, 10, …), so gibt es davon offenbar[1] weniger als von den natürlichen Zahlen (1, 2, 3, 4, …). Von den "runden" Zahlen (1, 10, 100, 1000, …) gibt es dann noch weniger. Wie mag es wohl mit den Primzahlen aussehen?
Es gibt so viele Primzahlen, daß 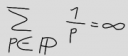
Häh?
OK, der Reihe nach; zuerst stellt sich die Frage, was da eigentlich steht. Das ist relativ einfach. Wenn wir alle Primzahlen nehmen (pϵP), zu jeder den Kehrwert bilden (1/p), und diese Kehrwerte dann aufsummieren (Ʃ), dann wird das Ergebnis unendlich groß. Auf den ersten Blick ist das vielleicht nicht verwunderlich; immerhin addieren wir unendlich viele Zahlen, die alle positiv sind.
Wenn wir aber statt 1/p die reziproken Zweierpotenzen addieren, dann ist das Ergebnis durchaus endlich: 1/2+1/4+1/8+…=1. Warum? Naja, 1/2 ist die Hälfte von 1; 1/4 ist die Hälfte von dem, was dann noch zu 1 fehlt, und so weiter:
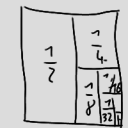
Wenn die Zahlen, deren Kehrwerte ich addiere, also schnell genug größer werden, dann kann die Reihe[3] konvergieren, also eine endliche Zahl als Ergebnis haben. Daß die Reihe der reziproken Primzahlen divergiert, bedeutet also, daß sie nicht sehr schnell größer werden — daß es also recht viele von ihnen gibt.
Langsam
Was heißt nicht sehr schnell? Nun, die Reihe der reziproken natürlichen Zahlen, 1+1/2+1/3+1/4+…, divergiert, i.e. die natürlichen Zahlen wachsen in diesem Sinne langsam. Die Quadratzahlen wachsen dagegen schnell, 1+1/4+1/9+1/16+… konvergiert nämlich[4] — nimmt man stattdessen dritte oder vierte Potenzen, so wachsen die Zahlen natürlich schneller, und die Reihen konvergieren auch. Man kann zeigen, daß Ʃ1/nr immer konvergiert, solange r nur größer als 1 ist. Es reicht, r=1,001 (oder noch kleiner) zu wählen. Das heißt, daß die Folge der Primzahlen tatsächlich sehr langsam wachsen muß, damit die Reihe divergiert.
An's Eingemachte
Behaupten kann man viel, wenn der Tag lang ist. Mathematiker wollen aber immer Beweise dafür sehen. Der, den ich hier vorführen möchte, stammt von dem berühmten Ungarn Erdős. Ich folge dabei dem Buch von Aigner und Ziegler[5].
Der Beweis ist wieder ein Widerspruchsbeweis, i.e. wir nehmen an, daß die Behauptung gerade nicht stimmt, rechnen ein bißchen herum und finden dabei einen Widerspruch. Daraus folgt dann, daß die Annahme falsch war.
Nehmen wir also an, daß die Reihe konvergiert. Wenn wir nun die ersten Summanden überspringen, dann wird die Gesamtsumme kleiner, und wenn wir genügend Summanden überspringen, können wir die Gesamtsumme kleiner als 1/2 machen.[6]
Wählen wir also k genügend groß, und denken wir uns noch irgendeine Zahl N aus, mit der wir die ganze Ungleichung multiplizieren, dann gilt:
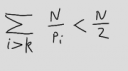
Wenn wir jetzt alle Zahlen betrachten, die nicht größer sind als N, dann gibt es solche, die sich durch eine Primzahl teilen lassen, die in unserer verkürzten Reihe vorhanden ist; ihre Anzahl wollen wir b nennen. Und es gibt solche, die nur Primteiler besitzen, die unter den ersten k Primzahlen sind und deswegen nicht in der verkürzten Reihe vorkommen; ihre Anzahl sei s. Weil alle Zahlen entweder zu der einen oder anderen Kategorie gehören müssen, ist s+b=N.
Wie groß ist b? Nun, für eine Primzahl pi gibt es  Zahlen, die durch sie teilbar sind. Wenn wir diesen Ausdruck über alle Primzahlen summieren, dann liegen wir vielleicht zu hoch, aber sicher nicht zu niedrig[7].
Zahlen, die durch sie teilbar sind. Wenn wir diesen Ausdruck über alle Primzahlen summieren, dann liegen wir vielleicht zu hoch, aber sicher nicht zu niedrig[7].
Wenn wir also summieren, dann steht wieder unsere Ungleichung von oben da, und es gilt: b < N/2.
Wie sieht es für s aus? Das geht anders, und zwar so: Wir schreiben jede Zahl n, die zu s zählt, als n=a·q2. Dabei ist a das Produkt aller Primfaktoren, die in n nur einmal vorkommen. Zum Beispiel ist 150=2·3·5·5, also a=2·3=6 und q=5.
Um die Frage zu klären, wie groß s ist, müssen wir also überlegen, wie viele verschiedene a und q es gibt. Das ist einfach: in a kommt jede Primzahl einmal oder keinmal vor, das sind zwei Möglichkeiten pro Primzahl. Da für s nur die ersten k Primzahlen in Frage kommen, sind das 2·2·2…=2k Möglichkeiten. Bei q machen wir es uns ganz einfach: q2 ≤ n, und n ≤ N, also q ≤ √N.
Damit ist s ≤ 2k√N.
Widerworte
Am Anfang hatten wir uns ja ein N ausgedacht, aber alle Überlegungen waren völlig allgemein. Wir können uns jetzt also noch umentscheiden und zum Beispiel N=22k+2 nehmen. Dann ist s ≤ s2k+1 (Einsetzen in die letzte Gleichung vom vorigen Absatz), also kleiner als N/2.
Weil b aber auch kleiner als N/2 ist, muß s+b kleiner als N sein.
Am Anfang hatten wir aber gesehen, daß s+b gerade gleich N ist. Beides gleichzeitig geht nicht, und da haben wir unseren Widerspruch.
Ende
Also, lieber unbekannter Google-User: es gibt nicht nur unendlich viele, sondern sogar verdammt viele Primzahlen, und die kann ich Dir unmöglich alle aufzählen.
Noten
[1] Ganz so einfach ist die Sache eigentlich nicht, dann auf eine sehr intuitive[2] Art gibt es gleich viele gerade und natürliche Zahlen. Das hört sich jetzt seltsam an, weil ja jede gerade Zahl eine natürliche ist, es aber auch natürliche Zahlen gibt, die nicht gerade sind — die ungeraden eben. Man kann aber von unendlichen Mengen durchaus einige Elemente wegnehmen, ohne daß die Menge kleiner würde.
In der Tat läßt sich diese Eigenschaft als Definition von unendlich verwenden.
[2] Vielleicht schreibe ich dazu noch einen Eintrag.
[3] Eine Reihe ist, vereinfacht gesagt, eine Summe unendlich vieler Zahlen.
[4] Und zwar gegen π2/6.
[5] Dieses Buch, das in Anlehnung an eine Idee von Erdős Das BUCH der Beweise heißt, kann man gar nicht genug loben. Deswegen wandert es jetzt erstmal in meine Sidebar.
[6] Das ist eine Eigenschaft von Grenzwerten. Letztlich ist der Grund der, daß die Reihe sich an ihr Ergebnis heranschleicht.
[7] Zu hoch deshalb, weil wir einiges doppelt zählen: 6 ist zum Beispiel durch 2 und 3 teilbar, und wir würden sie einmal bei den Vielfachen von 2, einmal bei denen von 3 zählen.
Kommentare deaktiviert für Wie viele?