JAN
2006
Beim letzten Mal haben wir gesehen, daß es Landkarten gibt, die mit weniger als vier Farben nicht gezeichnet werden können. Mit anderen Worten: wenn es eine Zahl n gibt, so daß mit n Farben beliebige Landkarten gezeichnet werden können, dann muß n≥4 sein.
Befindlichkeiten
Bevor wir nun untersuchen, ob wir auch eine obere Schranke für n finden können, wollen wir uns noch um einen anderen Aspekt kümmern: Wenn der kaiserliche Kartograph die Farben für die Karte aussucht, dann kann es vorkommen, daß die Landesfürsten mit den ihnen zugedachten Farben nicht zufrieden sind. Der eine hätte lieber Grün als Rot, dem anderen ist das Blau zu dunkel, und so weiter. Stattdessen die Fürsten ihre Farben aussuchen zu lassen, ist aber auch keine gute Idee: nachher müssen alle Länder in Gold dargestellt werden, und man erkennt überhaupt nichts mehr.
Deswegen hat sich der Kartograph folgende Regel ausgedacht: Jeder Landesfürst soll eine Liste mit k Farben, die ihm genehm sind, zusammenstellen. Die endgültige Auswahl der Farben aus diesen Listen nimmt der Kartograph dann selbst vor. Wie muß der Kartograph nun k wählen, damit er die Karte auf jeden Fall zeichnen kann? Wichtig ist dabei natürlich, daß k schon feststehen muß, bevor die Fürsten ihre Farben ausgesucht haben — unabhängig von deren Wahl muß die Karte machbar sein.
Mit und ohne Liste
Klar ist, daß k nicht kleiner als m sein kann, wenn für die vorliegende Karte mindestens m Farben benötigt werden; es wäre ja möglich, daß alle Fürsten zufällig die gleichen Listen abliefern — dann können nicht plötzlich weniger Farben als bei freier Farbwahl (für den Kartographen) nötig sein. Nun liegt der Verdacht nahe, daß k=m sein muß. Wenn alle Fürsten die gleiche Farbauswahl treffen, ist das naheliegend; anderenfalls kommen ja nur noch mehr Farben hinzu. Sechs Listen mit je zwei Farben enthalten zum Beispiel mindestens zwei Farben, es könnten aber auch mehr sein. Und wenn ich die Karte mit (beispielsweise) zwei Farben zeichnen kann, dann sollten sechs Listen mit je zwei Farben ja kein Problem sein. Wie gut, daß der Kartograph noch den kaiserlichen Mathematiker aufgesucht hat, bevor er die Boten zum Einsammeln der Farblisten ausschickte.
Weil unser Kartograph zu den Zeiten lebte, in denen noch gezaubert wurde, kann ich Euch leider keine echten Karten zeigen: sie sind alle durch die lange Zeit und die schädlichen Einflüsse der Zaubersprüche zerfallen. Stattdessen habe ich eine Karte von Obervolta, der Elfenbeinküste, Ghana, Togo, Benin und Atlantis ausgesucht. Na gut, Atlantis hat die Zaubersprüche auch nicht überstanden, da ist jetzt nur noch der Ozean. Das ändert aber an dem Problem nichts. Eine weitere Besonderheit von damals können wir heute nicht mehr sehen: die vier Länder in der Mitte hatten keine gemeinsamen Grenzen, weil die Zauberer für bodenlose Gräben zwischen ihnen gesorgt hatten. Deshalb können wir die Karte ganz einfach mit nur zwei Farben zeichnen:
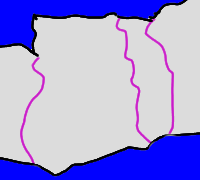
Atlantis und Obervolta werden blau, die anderen vier Länder weiß.
Wie wir — und der kaiserliche Kartograph — oben angenommen haben, sollte es also ausreichen, wenn jeder Landesfürst zwei Farben zur Auswahl angibt. Was aber, wenn das Ergebnis so aussieht?
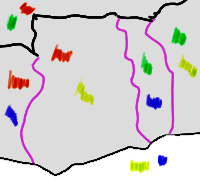
Obervolta will Rot oder Grün, Atlantis Gelb oder Blau, und so weiter. Jetzt haben wir ein Problem: Wir könnten Obervolta rot und Atlantis blau zeichnen, aber dann bleibt für die Elfenbeinküste keine Farbe übrig. Wenn Obervolta grün und Atlantis gelb wird, gibt es das gleiche Problem mit Benin. Die anderen beiden Kombinationen gehen auch nicht, weil dann entweder für Ghana oder Togo keine Farbe mehr bleibt.
Facit
Unsere Vermutung war also falsch: es gibt Karten, die sich mit m Farben vom Kartographen zeichnen lassen, nicht aber dann, wenn jeder Landesfürst eine Liste von m Farben zur Auswahl stellt, obwohl dann ja insgesamt mehr Farben zur Verfügung stehen. Umgekehrt ist aber jede Karte, die mit Farblisten zu je k Einträgen zu zeichnen ist, auch mit k Farben vom Kartographen zu zeichnen.
0:47 Kommentare deaktiviert für Bunte Karten IIvon kirjoittaessani