kirjoittaessani

Heute hat hier jemand falsche mathematische beweise lustige gesucht. Über die Wortstellung sehe ich ja großzügig hinweg, aber falsche Beweise?
Hier gibt es natürlich nur richtige Beweise. Diese Impertinenz!

Beim letzten Mal haben wir gesehen, daß es Landkarten gibt, die mit weniger als vier Farben nicht gezeichnet werden können. Mit anderen Worten: wenn es eine Zahl n gibt, so daß mit n Farben beliebige Landkarten gezeichnet werden können, dann muß n≥4 sein.

Befindlichkeiten

Bevor wir nun untersuchen, ob wir auch eine obere Schranke für n finden können, wollen wir uns noch um einen anderen Aspekt kümmern: Wenn der kaiserliche Kartograph die Farben für die Karte aussucht, dann kann es vorkommen, daß die Landesfürsten mit den ihnen zugedachten Farben nicht zufrieden sind. Der eine hätte lieber Grün als Rot, dem anderen ist das Blau zu dunkel, und so weiter. Stattdessen die Fürsten ihre Farben aussuchen zu lassen, ist aber auch keine gute Idee: nachher müssen alle Länder in Gold dargestellt werden, und man erkennt überhaupt nichts mehr.
Deswegen hat sich der Kartograph folgende Regel ausgedacht: Jeder Landesfürst soll eine Liste mit k Farben, die ihm genehm sind, zusammenstellen. Die endgültige Auswahl der Farben aus diesen Listen nimmt der Kartograph dann selbst vor. Wie muß der Kartograph nun k wählen, damit er die Karte auf jeden Fall zeichnen kann? Wichtig ist dabei natürlich, daß k schon feststehen muß, bevor die Fürsten ihre Farben ausgesucht haben — unabhängig von deren Wahl muß die Karte machbar sein.

Mit und ohne Liste

Klar ist, daß k nicht kleiner als m sein kann, wenn für die vorliegende Karte mindestens m Farben benötigt werden; es wäre ja möglich, daß alle Fürsten zufällig die gleichen Listen abliefern — dann können nicht plötzlich weniger Farben als bei freier Farbwahl (für den Kartographen) nötig sein. Nun liegt der Verdacht nahe, daß k=m sein muß. Wenn alle Fürsten die gleiche Farbauswahl treffen, ist das naheliegend; anderenfalls kommen ja nur noch mehr Farben hinzu. Sechs Listen mit je zwei Farben enthalten zum Beispiel mindestens zwei Farben, es könnten aber auch mehr sein. Und wenn ich die Karte mit (beispielsweise) zwei Farben zeichnen kann, dann sollten sechs Listen mit je zwei Farben ja kein Problem sein. Wie gut, daß der Kartograph noch den kaiserlichen Mathematiker aufgesucht hat, bevor er die Boten zum Einsammeln der Farblisten ausschickte.

Weil unser Kartograph zu den Zeiten lebte, in denen noch gezaubert wurde, kann ich Euch leider keine echten Karten zeigen: sie sind alle durch die lange Zeit und die schädlichen Einflüsse der Zaubersprüche zerfallen. Stattdessen habe ich eine Karte von Obervolta, der Elfenbeinküste, Ghana, Togo, Benin und Atlantis ausgesucht. Na gut, Atlantis hat die Zaubersprüche auch nicht überstanden, da ist jetzt nur noch der Ozean. Das ändert aber an dem Problem nichts. Eine weitere Besonderheit von damals können wir heute nicht mehr sehen: die vier Länder in der Mitte hatten keine gemeinsamen Grenzen, weil die Zauberer für bodenlose Gräben zwischen ihnen gesorgt hatten. Deshalb können wir die Karte ganz einfach mit nur zwei Farben zeichnen:

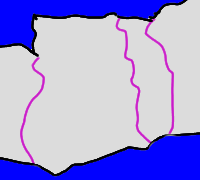
Atlantis und Obervolta werden blau, die anderen vier Länder weiß.

Wie wir — und der kaiserliche Kartograph — oben angenommen haben, sollte es also ausreichen, wenn jeder Landesfürst zwei Farben zur Auswahl angibt. Was aber, wenn das Ergebnis so aussieht?

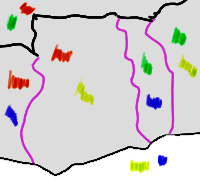
Obervolta will Rot oder Grün, Atlantis Gelb oder Blau, und so weiter. Jetzt haben wir ein Problem: Wir könnten Obervolta rot und Atlantis blau zeichnen, aber dann bleibt für die Elfenbeinküste keine Farbe übrig. Wenn Obervolta grün und Atlantis gelb wird, gibt es das gleiche Problem mit Benin. Die anderen beiden Kombinationen gehen auch nicht, weil dann entweder für Ghana oder Togo keine Farbe mehr bleibt.

Facit

Unsere Vermutung war also falsch: es gibt Karten, die sich mit m Farben vom Kartographen zeichnen lassen, nicht aber dann, wenn jeder Landesfürst eine Liste von m Farben zur Auswahl stellt, obwohl dann ja insgesamt mehr Farben zur Verfügung stehen. Umgekehrt ist aber jede Karte, die mit Farblisten zu je k Einträgen zu zeichnen ist, auch mit k Farben vom Kartographen zu zeichnen.

Auf politischen Landkarten verwendet man gerne Farben, um die einzelnen Staaten voneinander abzugrenzen. Wie viele verschiedene Farben man dafür braucht, hängt natürlich von der Karte, die man zeichnen möchte, ab.
Was aber, wenn ich einen Tuschekasten für Kartographen zusammenstellen möchte? Kann ich so viele Farben in den Kasten packen, daß meine Kunden damit auf jeden Fall auskommen — gleich, welche Karte sie zeichnen wollen?

Wenn zwei Länder schon dann unterschiedliche Farben erhalten sollen, wenn sie nur einen einzigen Punkt gemeinsam haben, dann ist die Antwort nein: im Reich des Tortenkaisers haben alle Königreiche einen Punkt gemeinsam, und deshalb brauchen die kaiserlichen Kartographen immer so viele Farben, wie es Könige gibt:

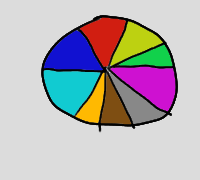
Wenn unterschiedliche Farben aber nur für solche Länder nötig sind, die tatsächlich ein Stück Grenze gemeinsam haben — vielleicht nur ein paar Meter — dann kann die Sache schon anders aussehen.

Wir haben jetzt zwei Aufgaben vor uns: zum einen wollen wir eine obere Schranke bestimmen, also eine Zahl von Farben, mit der wir auf jeden Fall auskommen; im Moment ist zwar nicht klar, ob so eine Zahl überhaupt existiert, aber davon lassen wir uns natürlich nicht aufhalten.
Zum anderen suchen wir auch eine Zahl von Farben, die (für zumindest eine denkbare Karte) zu klein ist. Diese Zahlen sollen natürlich so dicht wie möglich beieinander liegen, damit wir die kleinste Zahl von Farben, die auf jeden Fall ausreicht, gut eingrenzen können, und nicht übermäßig viele Farben in den Kasten packen.

Für heute soll der einfachere Teil genügen:

Untere Schranke

Um zu zeigen, daß n Farben zu wenig sind (und unser Tuschekasten also mindestens n+1 Farben enthalten muß), genügt es, eine Karte zu finden, die mit n Farben nicht mehr den Regeln entsprechend gezeichnet werden kann. Betrachten wir diese Karte von Luxemburg,

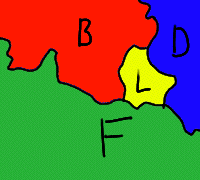
so stellen wir fest, daß wir hier vier Farben benötigen — jedes der vier abgebildeten Länder ist jedem anderen benachbart, und so braucht jedes auch seine eigene Farbe.

Einen Kasten mit nur drei Farben können wir also nicht verkaufen; festzustellen, ob es einen ausreichenden Kasten gibt, und wie groß dieser sein müßte, ist etwas schwieriger; deshalb hat das noch ein paar Tage Zeit.

Manchmal kommt es vor, daß man eine Reihe aufeinanderfolgender Zahlen addieren muß. Das ist zwar nicht schwierig, aber zeitraubend und recht eintönig. Zum Glück hat Gauß dafür eine Formel angegeben: Die Summe der ersten n natürlichen Zahlen ist gleich n(n+1)/2.
Der Legende nach ist Gauß als Schüler auf dieses Ergebnis gekommen, als er die Zahlen von Eins bis Hundert addieren sollte. Diese Rechnung dauert natürlich einige Zeit, aber seine Formel liefert ganz schnell 100·101/2=5050.

Wie kann man soetwas nun beweisen? Einfach nachrechnen funktioniert nur für gegebene Werte von n, zum Beispiel 1+2+3+4=10, 4·5/2=10 (stimmt!) — ein allgemeiner Beweis, daß die Formel für alle n gilt, ist das nicht.

Dafür haben sich die Mathematiker einen sehr nützlichen Trick einfallen lassen. Er funktioniert wie das Besteigen einer langen Leiter: auch wenn ich nicht genau weiß, wie viele Sprossen die Leiter hat, komme ich auf jeden Fall oben an, wenn ich zuerst vom Boden auf die unterste Sprosse und dann immer von einer Sprosse auf die nächste steige.

Also weisen wir zunächst die Gültigkeit der Formel für n=1 nach. Das ist nachgerade lächerlich einfach — die Summe der ersten einen natürlichen Zahl (was ein Satz) ist 1, und 1·2/2=1 ist auch klar.

Jetzt stehen wir also auf einer Sprosse und müssen auf die nächste klettern. Mit anderen Worten: wir müssen die Gültigkeit der Formel für die Zahl n+1 nachweisen unter der Voraussetzung, daß sie für n richtig ist. Wenn man das große Sigma(∑) als Zeichen für die Summe verwendet, dann sieht das so aus:

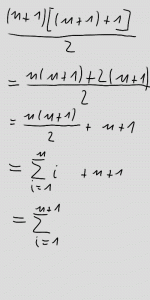
Man formt den Ausdruck etwas um und wendet zwischen der dritten und vierten Zeile die Formel für die Zahl n an — und das war es auch schon.

Diese Beweismethode nennt man vollständige Induktion (manchmal auch nur Induktion). Der meist sehr einfache Beweis für n=1 heißt Induktionsanfang, der Schritt von n auf n+1 Induktionsschluß oder Induktionsschritt. Außerdem gibt es noch die Induktionsannahme (auch Induktionsvoraussetzung), das ist die Annahme, daß die Formel für die Zahl n schon bewiesen sei.

Heute möchte ich mich mit einem Thema beschäftigen, das bei den meisten Menschen kein gutes Ansehen genießt: Mathematik. (Halt! Nicht wegklicken!)
Dabei soll es nicht um lustige Zahlenspielereien oder nützliche Rechenregeln gehen; vielmehr geht es mir um die Schönheit, die mathematische Aussagen und Beweise an den Tag legen, wenn man sie nicht als Mittel, sondern als Zweck betrachtet.
Die Idee dabei ist, einzelne Themen herauszugreifen und (hoffentlich) auch für Mathematik-Abstinenzler verständlich darzustellen.

Zu Anfang soll es um Primzahlen gehen. Die haben viele Vorteile: die meisten Menschen wissen, was Primzahlen sind; sie haben keine direkte Anwendung außerhalb der Mathematik (so daß man nicht so leicht abgelenkt wird); und man kann viele lustige Dinge mit ihnen anstellen.

Wenn der Mathematiker einen neuen Begriff einführt, dann tut er das mit einer Definition, die genau sagt, wie der Begriff zu verstehen ist. Primzahlen sind bekanntlich Zahlen, die nur durch Eins und sich selbst teilbar sind. Etwas genauer kann man definieren:
Eine natürliche Zahl n, deren Teilermenge genau zwei Elemente enthält, heißt Primzahl.
Daraus folgt, daß die Eins keine Primzahl ist, denn ihre Teilermenge enthält nur ein Element. Die umgangssprachliche Formulierung nur durch Eins und sich selbst teilbar ist da etwas unklar, was später zu Verwirrung führen könnte.

Welche konkreten Zahlen sind denn nun prim? Die ersten sind schnell aufgezählt: 2, 3, 5, 7, 11, 13, ...
Und wie geht es weiter? Vor allem: ist irgendwann Schluß, oder gibt es unendlich viele Primzahlen? Einerseits ist nicht recht einzusehen, warum es unendlich viele natürliche Zahlen, aber nur endlich viele Primzahlen geben soll; andererseits ist unsere Unfähigkeit, uns eine Welt mit endlich vielen Primzahlen vorzustellen, ein ziemlich schwaches Argument. Es muß also ein Beweis her. Vorher formulieren wir noch schnell einen Satz, der die zu beweisende Aussage formuliert:
Es gibt unendlich viele Primzahlen.
Eine häufig verwandte Methode ist die des Beweises durch Widerspruch: man nimmt einfach das Gegenteil der Behauptung an und leitet daraus einen Widerspruch her. Wenn die Schlußfolgerungen alle einwandfrei sein, muß die ursprüngliche Annahme falsch sein — und damit die Behauptung wahr.
Wir nehmen also an, es gäbe nur endlich viele Primzahlen, sagen wir n Stück. Diese numerieren wir durch: p₁, p₂, ..., p_n. Betrachten wir nun die Zahl x, die um eins größer als das Produkt aller Primzahlen ist: x=p₁p₂...p_n+1. Jede Zahl besitzt einen Primteiler, also auch x — das ist aber ein Widerspruch, denn p₁p₂...p_n ist ja per Konstruktion durch alle Primzahlen teilbar; zwei aufeinanderfolgende Zahlen haben aber keine gemeinsamen Teiler (außer 1).
[Das sieht man so: wenn n und n+1 beide durch p teilbar sind, dann gibt es x und y, so daß n=xp und n+1=yp, also xp+1=yp. Damit ist aber (y–x)p=1, also auch Eins durch p teilbar => Widerspruch, denn Eins besitzt (außer sich selbst) keine Teiler.]

Die Annahme, es gebe nur endlich viele Primzahlen, führt also auf einen Widerspruch, so daß es unendlich viele Primzahlen geben muß, q.e.d.