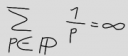kirjoittaessani

Earlier this week, Slashdot published the news that a three-dimensional equivalent of the Mandelbrot set has been found. Visiting Daniel White's page, not only did I find an explanation, but also unprecedented images -- and I knew immediately that I would like to create such images myself.

Fractured

The class of objects to which the Mandelbrot and the new Mandelbulb belong is called fractals. What are fractals, anyway? Well, a fractals in an object with a dimension that is not an integer. At first glance, it is not quite clear what this means: an object is either one-dimensional, such as a line; or a sheet of paper, which has two dimensions (ignoring its thickness); or, for example, a cube with three dimensions. But two and a half?

If we look at the dimension of a vector space, this is, indeed, impossible: there, one would simply count the (independent) directions that are to be found in a given object, and name there number the object's dimension: if there is just length (such as on a piece of string), the dimension is one. The living room has length, width, and height, thus it is three-dimensional.

But there is a different way: let us take a ball that is large enough to hide the piece of string. For a one-meter string, we would need a ball one meter in diameter. Then, try with a ball half that size: we would need two to cover the string. If we tried with ten-centimeter balls, we would need ten of them, and so on.

That does not work for my living-room, however: I could put the whole room into a large ball of, say, five meters; but I would need many more than just five balls of one meter each -- more than a hundred, in fact. That is, the dimension of an object tells us how quickly the number of balls grows when the balls themselves shrink. For a one-dimensional object, 2 balls of size 1/2 are sufficient, for something three-dimensional, we would need 8, or 2³.

Now, let us turn around and use this counting as a definition: a chessboard is two-dimensional precisely because we need  64=8² squares of size 1/8 to cover it.

Erasing

What would an object need to look like to make a fractional number drop out of this computation? Let us make a little experiment. You only need a sheet of paper, a pencil, an eraser, and maybe a ruler (I did without). First, draw a straight line, like this:

Then, take the eraser to remove the middle third of the line:

Erase the middle third of the two remaining lines as well:

And so on -- in principle, you can continue indefinitely. That is, as long as your eraser is fine enough.

What happens if you try to cover your creation with balls? Start with one that is large enough to cover all those little dashes. If you then try balls a third of its size, you do not need three of them -- instead, two are sufficient: one for the left side, one for the right. You have removed everything in the middle with your eraser, after all. Using balls of diameter 1/3, only 2=3^0.63 of them are enough to cover the drawing. So you could say your little piece of art has a dimension of 0.63. This is not as weird as it may look at first glance: There is an enormous number of dots, most of which are very close together.  Isolated dots would have a dimension of 0; and dots that are infinitely close together form a line of dimension 1. Our result is somewhere inbetween, which should hardly come as a surprise.

The Mandelbrot set is similar: regardless of how far we magnify parts of it, there are ever finer structures appearing.In principle, this is true for the Mandelbulb above; however, the picture has been rendered with simplified equation, so only the largest knobs are visible: it is like throwing away the erasor after the first two steps.

Appearing soon

During the next few days, I would like to show how to calculate the Mandelbrot set, and the new Mandelbulb. Hopefully, there will also be more pictures, and perhaps a movie or two.

[Edit: Typos]

Zum Tagesabschluß habe ich noch etwas heiteres, nämlich eine Suchanfrage: warum muss man bei primzahlen die vielfachen fon 11 nicht streichen?, will ein unbekannter Besucher wissen.

Da kann ich nur sagen: die Frage ist falsch gestellt. Wenn man mit dem Sieb des Eratosthenes Primzahlen bestimmen will, sind die Vielfacher von elf durchaus zu streichen -- genauso wie die aller anderen Primzahlen. Sind allerdings nur die Primzahlen bis N=100 gefragt, kann man nach der sieben aufhören: es genügt immer, bis zur Wurzel von N (hier also 10) zu prüfen.

Das sieht man so: angenommen, es gibt einen Teiler von n≤N (nennen wir ihn a), mit a>√N. Dann ist aber auch b = n/a ≤ N/a < N/√N = √N, also b<√N, Teiler von n; und so erkennen wir auch dann, daß n nicht prim ist, wenn wir nur bis √N prüfen.

Gute Nacht.

Today, I would like to present a funny -- if somewhat useless -- mathematical toy.

Originally, I wanted to create some sleak pictures to illustrate a graphic method for multiplying decimal numbers -- but someone has been faster than me, posting a video at Youtube.

Therefore, I leave my pencil alone. I shall merely add that this method works in exactly the same way as the usual pencil-and-paper way does.

Bei der Bewertung von Rudolf Kippenhahns Verschlüsselten Botschaften finde ich mich in einem Dilemma wieder; denn die größte Schwäche des Buchs ist gleichzeitig seine größte Stärke: der Autor verzichtet beinahe völlig auf Mathematik. Daher kann er moderne Schlüsselverfahren lediglich streifen. Wer hier einen Einblick gewinnen will, ist etwa mit Schneiers Applied Cryptography besser bedient.

Dem mathematischen Laien allerdings hat Kippenhahns Werk einiges zu bieten. Klassische Verfahren wie der Caesar-Chiffre werden recht ausführlich erklärt, und auch einige weniger bekannte Methoden wie etwa eine Transposition mittels einer drehbaren Schablone finden Erwähnung.
Einen recht breiten Raum nimmt die erste Hälfte des 20. Jahrhunderts ein, hier besonders die Enigma. Neben der legitimen Ver- und Entschlüsselung stellt der Autor auch die Schwächen der Verfahren und die daraus resultierenden Angriffspunkte vor.

Die theoretischen Abschnitte sind immer wieder unterbrochen von plastisch erzählten historischen Szenen; so bleibt die Lektüre auch dann abwechslungsreich, wenn die Theorie wegen mathematischer Vorkenntnisse einige Längen aufweist, oder aber mangels solcher Kenntnisse sehr trocken wird.

Zum Schluß werden auch moderne Verfahren kurz angerissen, und man erfährt etwa, wie Public-Key-Kryptographie prinzipiell funktioniert, oder die Geheimzahl einer Scheckkarte abgesichert wird.
Unter dem Strich ist das Buch eine gute Einführung in die Kryptologie; wer sich mit den Verfahren bereits etwas auskennt, der hat immerhin eine kurzweilige Lektüre, bei der er auch noch ein paar interessante historische Details lernen mag.

[Diese Rezension ist auch bei Lovelybooks verfügbar (derzeit leider nur für dort registrierte Mitglieder]

What would we do without referrers? I do not really know, but bloggers would have to do without a lot of funny search requests.

A few days ago, someon was looking for a Rechenregel wie man erkennt durch welche Zahlen eine Zahl teilbar ist. That roughly translates as rule how to recognize by which numbers a number is divisible. Anyway, I am happy to provide a few. All rules are equivalencies, that is the given number is divisible if the rule is fulfilled; otherwise, it is not divisible.

1. every number is divisible by one 🙂
2. the final digit is divisible by two
3. the cross total (sum of digits) is divisible by three
4. the number comprised of the final two digits is divisible by four
5. the final digit is zero or five
6. both rules 2 and 3 hold
7. double the final digit and subtract it from the rest of the number; the result is divisible by seven; e.g. 203: 20-2*3=14 is divisible
8. the number comprised of the final three digits is divisible by eight
9. the cross total is divisible by nine
10. the final digit is zero
11. the alternating sum of digits is divisible by eleven, e.g. 135795: 1-3+5-7+9-5=0 is divisible
12. rules 3 and 4 hold
13. quadruple the final digit and add it to rest of the number; the result is divisible by thirteen; e.g. 403: 40+4*3=52; it is useful to apply the rule again: 5+4*2=13 isdivisible, so 52 is, and therefore 403 as well.

Well, that should suffice for now.

Fermats Letzter Satz ist ein gutes Buch. Es fällt mir schwer, einen kritisierenswerten Punkt zu finden, und deshalb nehme ich einfach diesen: Der Titel ist irreführend. Nicht wirklich schlimm irreführend, aber die berühmte Fermat'sche Vermutung, daß nämlich die Gleichung aⁿ+bⁿ=cⁿ für n>2 keine positiven Lösungen habe, ist eher der Aufhänger als das Hauptthema des Buches.

Singh liefert hier einen Streifzug durch die Mathematik, der im klassischen Griechenland beginnt und bis in die Gegenwart reicht. Dabei hat er beileibe kein mathematisches Lehrbuch geschrieben, nicht einmal ein Mathematikbuch für Laien. Vielmehr zeigt er, wie Mathematiker denken und arbeiten, wie sich die Arbeitsweise im Laufe der Zeit geändert hat, und was sie antreibt.

Dabei nehmen Fermat und Wiles (der den Satz bewiesen hat) natürlich einen größeren Raum ein, doch Singh betrachtet auch noch eine Vielzahl weiterer Persönlichkeiten. Auf mathematische Details verzichtet er hingegen fast völlig. Das betrifft nicht nur Wiles' Beweis (der immerhin über 100 Seiten in einer Fachzeitschrift füllt), sondern fast alle Beweise und sogar die meisten Sätze. Daher bleibt das Buch auch für mathematische Laien lesbar, wenngleich sich Leser mit entsprechender Vorbildung teils mehr Details wünschen mögen. Für letztere gibt es aber ein Literaturverzeichnis, das nicht nur auf weitere populärwissenschaftliche Werke, sondern auch auf mathematische Fachbeiträge verweist.

…das war vor einiger Zeit recht beliebt bei den Suchanfragen, die hierher führen. Im Moment steht 1000 als summe aufeinanderfolgender zahlen hoch im Kurs.

Also gut: einmal Schummeln für unfähige Anfänger. Ihr dürft jetzt alle hier abschreiben und Euch dann wundern, wenn Ihr die nächste Klausur verhaut.

Summa cum

Wir wollen also schreiben können k+(k+1)+…+l = 1000.
Vom ollen Gauß wissen wir ja, daß die Summe der Zahlen von 1 bis n gegeben ist als n(n+1)/2. Wie sieht das also aus, wenn wir von k+1 bis l summieren? Ganz einfach: wir rechnen erstmal von Eins bis l, ziehen dann aber die zu kleinen Zahlen wieder ab. Also:

1000 = l(l+1)/2 - k(k+1)/2.

Anders formuliert könnten wir auch l=k+n setzen und sagen, daß wir n aufeinanderfolgende Zahlen ab k +1 summieren wollen. Dann haben wir:

1000 = (k+n)·(k+n+1)/2 - k(k+1)/2

Multiplizieren wir das ganze mit 2 und vereinfachen ein bißchen, dann haben wir diese schöne Formel:

2000 = n(2k+n+1)

Gerade oder ungerade, das ist hier die Frage

Das bedeutet: um 1000 als Summe aufeinanderfolgender Zahlen schreiben zu können, müssen wir 2000 als Produkt zweier Zahlen, nämlich n und 2k+n+1schreiben. Dabei kann n gerade oder ungerade sein; da 2k+1 aber immer ungerade ist, wird 2k+n+1 genau dann gerade sein, wenn n ungerade ist.
Jetzt zerlegen wir 2000 in seine Primfaktoren und überlegen, auf wie viele Arten wir daraus einen geraden und einen ungeraden Faktor basteln können. 2000=2⁴·5³; die Faktoren 2 müssen immer zusammen vorkommen, sonst wären ja beide Teile gerade, die anderen können wir verteilen:

2000 = 16·125 = 80·25 = 400·5 = 2000·1

Das war's auch schon, mehr als diese Varianten gibt es nicht. Jetzt müssen wir nur noch feststellen, ob jedem Produkt auch eine Darstellung der Zahl 1000 entspricht, und wie diese jeweils aussieht.

Aufgezählt

Die Zahl der Summanden, die in der Formel mit n angegeben ist, kann also höchstens die Werte 1, 5, 16, 25, 80, 125, 400, 2000 annehmen. Die probieren wir jetzt der Reihe nach durch:
Ist n=1, dann folgt 2k+n+1=2000, also k=999. Das ist das, was die Mathematiker gerne als triviale Lösung bezeichnen: eine Möglichkeit, 1000 als Summe aufeinanderfolgender Zahlen zu schreiben, ist die einzige Zahl 1000 — eine Folge aus einer Zahl.

n=5 ist schon interessanter: 2k+n+1=400, also k=197, das heißt die Summe hat fünf Glieder und startet oberhalb von 197: 1000=198+199+200+201+202.

n=16 liefert 2k+n+1=125, also k=54. Damit ist 1000 = 55+56+…+69+70.

Aus n=25 folgt 2k+n+1=80 und k=27: 1000 = 28+29+…+52.

Dann haben wir noch n=80, also 2k+n+1=125, k=22: 1000 = 23+24+…+102.

Bei n=125 ist dann Schluß: dann wäre 2k+n+1=80, und diese Gleichung läßt sich durch kein positives k mehr erfüllen.

Zum Schluß

Auf eine Sache sollte ich noch eingehen: warum dürfen wir hier eigentlich ganz munter räsonieren und Teiler aufschreiben, nur um hinterher zu sagen: ätsch, 125 (und die größeren) waren nur ein Scherz? Wäre es nicht genauso möglich, daß unsere Methode nicht nur blinde Passagiere wie die 125 ausspuckt, sondern auch richtige Lösungen (meinetwegen n=17) verschluckt?

Nein, das geht zum Glück nicht: mathematische Argumente sind, wenn sie sauber verwendet werden, exakt. Daß wir trotzdem zunächst einige Zahlen bekommen haben, die wir dann doch wieder verwerfen mußten, liegt an dem Unterschied zwischen einer Folgerung und einer Äquivalenz: Wenn 1000 sich als die Summe der Zahlen k+1 bis k+n schreiben läßt, dann gelten die oben gemachten Überlegungen, und dann muß schließlich n ein Teiler von 2000 sein. Das heißt aber nicht, daß sich umgekehrt auch jede Zahl n, die Teiler von 2000 ist, automatisch in eine solche Summe verwandeln läßt. Dazu muß noch mehr gelten, n darf nämlich nicht nur irgendein Teiler von 2000 sein, sondern muß gerade komplementär zu 2k+n+1 sein. Wenn das nicht erfüllbar ist (z.B. für n=125), dann fallen die restlichen Überlegungen flach.

So, jetzt ist aber genug geschummelt.

[Edit: diverse Typos]

Referrer sind doch eine tolle Sache — so bekommt man erst mit, was die Be-sucher denn so alles suchen. Einer wollte neulich alle primzahlen aufgezählt haben.
Damit kann ich leider nicht dienen, denn es gibt eine ganze Menge Primzahlen — unendlich viele, um genau zu sein.

Viel

Geht es noch genauer? Unendlich ist ja nicht gleich unendlich. Nimmt man zum Beispiel nur die geraden Zahlen (2, 4, 6, 8, 10, …), so gibt es davon offenbar[1] weniger als von den natürlichen Zahlen (1, 2, 3, 4, …). Von den "runden" Zahlen (1, 10, 100, 1000, …) gibt es dann noch weniger. Wie mag es wohl mit den Primzahlen aussehen?
Es gibt so viele Primzahlen, daß

Häh?

OK, der Reihe nach; zuerst stellt sich die Frage, was da eigentlich steht. Das ist relativ einfach. Wenn wir alle Primzahlen nehmen (pϵP), zu jeder den Kehrwert bilden (1/p), und diese Kehrwerte dann aufsummieren (Ʃ), dann wird das Ergebnis unendlich groß. Auf den ersten Blick ist das vielleicht nicht verwunderlich; immerhin addieren wir unendlich viele Zahlen, die alle positiv sind.
Wenn wir aber statt 1/p die reziproken Zweierpotenzen addieren, dann ist das Ergebnis durchaus endlich: 1/2+1/4+1/8+…=1. Warum? Naja, 1/2 ist die Hälfte von 1; 1/4 ist die Hälfte von dem, was dann noch zu 1 fehlt, und so weiter:

Wenn die Zahlen, deren Kehrwerte ich addiere, also schnell genug größer werden, dann kann die Reihe[3] konvergieren, also eine endliche Zahl als Ergebnis haben. Daß die Reihe der reziproken Primzahlen divergiert, bedeutet also, daß sie nicht sehr schnell größer werden — daß es also recht viele von ihnen gibt.

Langsam

Was heißt nicht sehr schnell? Nun, die Reihe der reziproken natürlichen Zahlen, 1+1/2+1/3+1/4+…, divergiert, i.e. die natürlichen Zahlen wachsen in diesem Sinne langsam. Die Quadratzahlen wachsen dagegen schnell, 1+1/4+1/9+1/16+… konvergiert nämlich[4] — nimmt man stattdessen dritte oder vierte Potenzen, so wachsen die Zahlen natürlich schneller, und die Reihen konvergieren auch. Man kann zeigen, daß Ʃ1/n^r immer konvergiert, solange r nur größer als 1 ist. Es reicht, r=1,001 (oder noch kleiner) zu wählen. Das heißt, daß die Folge der Primzahlen tatsächlich sehr langsam wachsen muß, damit die Reihe divergiert.

An's Eingemachte

Behaupten kann man viel, wenn der Tag lang ist. Mathematiker wollen aber immer Beweise dafür sehen. Der, den ich hier vorführen möchte, stammt von dem berühmten Ungarn Erdős. Ich folge dabei dem Buch von Aigner und Ziegler[5].

Der Beweis ist wieder ein Widerspruchsbeweis, i.e. wir nehmen an, daß die Behauptung gerade nicht stimmt, rechnen ein bißchen herum und finden dabei einen Widerspruch. Daraus folgt dann, daß die Annahme falsch war.

Nehmen wir also an, daß die Reihe konvergiert. Wenn wir nun die ersten Summanden überspringen, dann wird die Gesamtsumme kleiner, und wenn wir genügend Summanden überspringen, können wir die Gesamtsumme kleiner als 1/2 machen.[6]

Wählen wir also k genügend groß, und denken wir uns noch irgendeine Zahl N aus, mit der wir die ganze Ungleichung multiplizieren, dann gilt:

Wenn wir jetzt alle Zahlen betrachten, die nicht größer sind als N, dann gibt es solche, die sich durch eine Primzahl teilen lassen, die in unserer verkürzten Reihe vorhanden ist; ihre Anzahl wollen wir b nennen. Und es gibt solche, die nur Primteiler besitzen, die unter den ersten k Primzahlen sind und deswegen nicht in der verkürzten Reihe vorkommen; ihre Anzahl sei s. Weil alle Zahlen entweder zu der einen oder anderen Kategorie gehören müssen, ist s+b=N.

Wie groß ist b? Nun, für eine Primzahl p_i gibt es Zahlen, die durch sie teilbar sind. Wenn wir diesen Ausdruck über alle Primzahlen summieren, dann liegen wir vielleicht zu hoch, aber sicher nicht zu niedrig[7].
Wenn wir also summieren, dann steht wieder unsere Ungleichung von oben da, und es gilt: b < N/2.

Wie sieht es für s aus? Das geht anders, und zwar so: Wir schreiben jede Zahl n, die zu s zählt, als n=a·q². Dabei ist a das Produkt aller Primfaktoren, die in n nur einmal vorkommen. Zum Beispiel ist 150=2·3·5·5, also a=2·3=6 und q=5.
Um die Frage zu klären, wie groß s ist, müssen wir also überlegen, wie viele verschiedene a und q es gibt. Das ist einfach: in a kommt jede Primzahl einmal oder keinmal vor, das sind zwei Möglichkeiten pro Primzahl. Da für s nur die ersten k Primzahlen in Frage kommen, sind das 2·2·2…=2^k Möglichkeiten. Bei q machen wir es uns ganz einfach: q² ≤ n, und n ≤ N, also q ≤ √N.

Damit ist s ≤ 2^k√N.

Widerworte

Am Anfang hatten wir uns ja ein N ausgedacht, aber alle Überlegungen waren völlig allgemein. Wir können uns jetzt also noch umentscheiden und zum Beispiel N=2^2k+2 nehmen. Dann ist s ≤ s^2k+1 (Einsetzen in die letzte Gleichung vom vorigen Absatz), also kleiner als N/2.

Weil b aber auch kleiner als N/2 ist, muß s+b kleiner als N sein.
Am Anfang hatten wir aber gesehen, daß s+b gerade gleich N ist. Beides gleichzeitig geht nicht, und da haben wir unseren Widerspruch.

Ende

Also, lieber unbekannter Google-User: es gibt nicht nur unendlich viele, sondern sogar verdammt viele Primzahlen, und die kann ich Dir unmöglich alle aufzählen.

Noten

[1] Ganz so einfach ist die Sache eigentlich nicht, dann auf eine sehr intuitive[2] Art gibt es gleich viele gerade und natürliche Zahlen. Das hört sich jetzt seltsam an, weil ja jede gerade Zahl eine natürliche ist, es aber auch natürliche Zahlen gibt, die nicht gerade sind — die ungeraden eben. Man kann aber von unendlichen Mengen durchaus einige Elemente wegnehmen, ohne daß die Menge kleiner würde.
In der Tat läßt sich diese Eigenschaft als Definition von unendlich verwenden.

[2] Vielleicht schreibe ich dazu noch einen Eintrag.

[3] Eine Reihe ist, vereinfacht gesagt, eine Summe unendlich vieler Zahlen.

[4] Und zwar gegen π²/6.

[5] Dieses Buch, das in Anlehnung an eine Idee von Erdős Das BUCH der Beweise heißt, kann man gar nicht genug loben. Deswegen wandert es jetzt erstmal in meine Sidebar.

[6] Das ist eine Eigenschaft von Grenzwerten. Letztlich ist der Grund der, daß die Reihe sich an ihr Ergebnis heranschleicht.

[7] Zu hoch deshalb, weil wir einiges doppelt zählen: 6 ist zum Beispiel durch 2 und 3 teilbar, und wir würden sie einmal bei den Vielfachen von 2, einmal bei denen von 3 zählen.

Es wird Zeit, sich noch einmal mit Landkarten zu beschäftigen. Wir haben bereits gesehen, daß ein Tuschekasten für Kartographen mindestens vier Farben enthalten muß. Außerdem braucht man dann, wenn für jedes Land eine Liste von Farben gebildet werden soll, höchstens mehr, niemals aber weniger Farben.
Noch offen ist aber die Frage, ob ich einen Tuschekasten zusammenstellen kann, mit dem jeder Kartograph für alle Karten auskommt.

Behauptung

Ich behaupte: ja, das geht. Fünf Farben reichen aus.
Mehr noch: es genügt sogar, wenn für jedes Land eine Liste mit fünf Farben zur Verfügung steht. (Wir hatten ja gesehen, daß das ein schwierigeres Problem ist.)

Induziert

Wie beweist man das am besten? Das Verfahren der vollständigen Induktion bietet sich hier an: Eine Karte mit nicht mehr als fünf Ländern kann ich natürlich immer mit fünf Farben zeichnen (Induktionsanfang). Wenn ich jetzt aus einer Karte mit n Ländern auf geschickte Weise ein Land eliminieren könnte, wäre ich schon am Ziel. Aber wie stellt man das an?
Als erstes greifen wir tief in die Trickkiste und fördern etwas zutage, das sich Warum einfach, wenn's auch kompliziert geht? nennt: wir beweisen schlichtweg etwas, das schwieriger (stärker) ist, und machen uns die Arbeit dadurch einfacher. Das hört sich seltsam an; der Grund liegt aber darin, daß wir uns sozusagen auf der Leiter von Sprosse zu Sprosse hangeln. Wenn wir alle Sprossen etwas höher einbauen, müssen wir zwar mit jedem Schritt etwas höher hinauf als bei unserer Originalleiter, aber wir starten ja auch jeden Schritt von einer höheren Sprosse aus.

Wirklich schwieriger wird nur die erste Sprosse; die ist aber bei Induktionsbeweisen kein wirkliches Problem. Zugegeben, ein bißchen hinkt die Analogie schon: wenn ich die Behauptung stärker mache, so kann der Beweis tatsächlich gleich schwer bleiben (wie bei der Leiter), er kann aber auch schwieriger oder einfacher werden. Hier wird er erfreulicherweise einfacher.

Weiter im Text

Weiter wollen wir annehmen, daß es höchstens Drei-Länder-Ecke gibt — aber keine Vier-, Fünf-, oder Noch-mehr-Länder-Ecke.

Wenn wir es doch einmal mit einer solchen Karte zu tun haben sollten, wollen wir einfach die Grenzen ein bißchen verschieben. Das ist nicht schlimm, weil das Problem dadurch nur schwieriger wird, die neue Lösung also auf jeden Fall auch Lösung des ursprünglichen Problems ist.

Behaupten kann man viel

Sehen wir uns eine Karte an, dann gibt es dort immer einen Ring von äußeren Ländern; hier sind es z.B. Washington, Oregon, Kalifornien, Arizona, New Mexico, Texas und so weiter.

Seien nun zwei benachbarte Länder dieses Rings bereits eingefärbt; jedes weitere Land auf dem Ring stelle eine Liste mit (mindestens) drei Farben bereit; jedes Land aus dem Inneren stelle eine Liste mit mindestens fünf Farben bereit.
Dann — so unsere Behauptung — können wir die gesamte Karte unter Benutzung dieser Listen einfärben.

Stärke

Diese Behauptung hat mit unserem ursprünglichen Ziel — der Einfärbung der Karte unter Benutzung von Fünfer-Farblisten — nicht mehr viel zu tun. Sie ist aber stärker: Wir behaupten jetzt, daß nur die inneren Länder noch Fünfer-Listen bereitstellen sollen; die Länder auf dem Ring liefern nur noch Dreier-Listen, zwei geben ihre Farbe sogar fest vor. Wenn wir die Karte unter diesen Bedingungen färben können, kommen wir mit Fünfer-Listen auf jeden Fall hin.

Aller Anfang ist leicht

Wenn nur drei Länder auf der Karte sind, so reichen uns die Farben auf jeden Fall: zweie sind ja schon gefärbt, und das dritte bietet uns eine Liste mit drei Farben an; egal, welche Farben durch die beiden Nachbarn belegt sind, eine bleibt immer frei.

Ein kleiner Schritt für einen Kartographen

Erinnern wir uns an die Vorgehensweise beim Induktionsschritt: wir müssen die Behauptung für eine Karte mit n Ländern beweisen, dürfen aber annehmen, sie sei für n-1 Länder, ja sogar für alle möglichen Karten mit weniger als n Ländern bereits bewiesen. Wir müssen also unsere große Karte auf eine (oder zwei) kleinere Karten zurückführen.
Nehmen wir nun an, zwei Länder aus dem äußeren Ring haben eine gemeinsame Grenze, die aber selbst nicht nach außen stößt; der Ring hat dann die Form einer Acht. Zaire und der Sudan sind ein Beispiel.

Jetzt können wir die Karte in zwei Teile zerlegen: die eine enthält Zaire, den Sudan, und alle weiter nördlich gelegenen Länder; die andere enthält ebenfalls Zaire und den Sudan, dazu aber die südlicheren Länder. Für Zaire und den Sudan vergeben wir jetzt je eine Farbe fest (etwa grün und rot); alle anderen Länder auf dem alten Ring haben Listen mit drei Farben, die inneren Länder deren fünf — so war ja die Voraussetzung. Dann gilt das aber auch für jede der beiden neuen "halben" Karten. Da diese kleiner sind, dürfen wir die Behauptung als bereits bewiesen ansehen. Beide kleinen Karten sind also mit den vorgegebenen Farben einfärbbar, und damit auch die gesamte Karte.
Das war es auch schon — mehr hatten wir gar nicht behauptet.

Unachtsam

Was nun, wenn der äußere Ring nicht die Form einer Acht hat?
Dann müssen wir die Zahl der Länder eben auf andere Art verringern. Nehmen wir die Karte der USA von oben, dann hat der äußere Ring dort nicht die Form einer Acht.

Angenommen, Washington sei bereits blau gefärbt. Auf dem Ring hat dieser Staat zwei Nachbarn: Idaho und Kalifornien. Angenommen, Idaho sei ebenfalls gefärbt (nach Annahme muß es ein Nachbar Washingtons auf dem Ring sein; es bleiben also nur CA oder ID). Dann entfernen wir jetzt probehalber Kalifornien von der Karte. Dadurch wird Nevada neu in den äußeren Ring aufgenommen — bei einer anderen Karte könnte natürlich auch eine ganze Reihe von Staaten dazukommen.
Nach Annahme hat Kalifornien (mindestens) eine Liste von drei Farben zur Verfügung gestellt; davon müssen mindestens zwei von Blau verschieden sein (sagen wir, Rot und Gelb). Diese beiden Farben streichen wir jetzt von der Farbliste Nevadas. Da die Liste vorher mindestens fünf Farben enthielt, bleiben also jetzt noch drei. Das heißt aber, daß die neue Karte (ohne Kalifornien) alle Voraussetzungen erfüllt, um vorschriftsmäßig gefärbt zu werden. Wenn wir jetzt noch eine Farbe für Kalifornien finden, sind wir fertig. Das ist aber leicht:
Nevada kann weder rot noch gelb sein, da wir diese Farben von der Liste gestrichen haben. Washington ist schon blau, und Arizona kann entweder Rot oder Gelb (oder eine andere Farbe) erhalten, aber nicht beide; deswegen bleibt eine der beiden Farben Rot und Gelb für Kalifornien.

Das war's, die Karte ist gefärbt!

Und sonst?

Im Falle der Farblisten ist Fünf tatsächlich die kleinste Zahl, die man finden kann. Margit Voigt hat ein Beispiel gefunden für eine Karte, die sich mit Vierer-Farblisten nicht immer einfärben läßt. Sie hat 238 Länder eingezeichnet.

Wenn es nur um den Tuschekasten geht, reichen dagegen sogar vier Farben. Der Beweis dafür ist allerdings leider viel zu lang und kompliziert für dieses Blog.

Der obige Beweis folgt übrigens dem Buch von Martin Aigner und Günther Ziegler, in dem sich — etwa auf Vordiplomniveau — eine ganze Reihe schöner Beweise findet.

Der Spiegel berichtet — nicht zum ersten Mal — über einen Bochumer Mathematiker, der die deutschen Zahlwörter ändern will: Einundzwanzig sei unlogisch, er möchte deshalb zwanzigeins einführen.
Der Artikel liest sich stellenweise, als ob der Untergang des Abendlandes oder doch wenigstens ein schlechtes Abschneiden bei der PISA-Studie drohte, wenn diese Änderung nicht durchgeführt wird. Ich habe da ein ganz anderes Problem: wo haben sie in dem Artikel nur die Smilies versteckt?