kirjoittaessani

Wirklich witzige Google-Anfragen kann ich aus letzter Zeit leider nicht vermelden. Festzustellen bleibt lediglich, daß sich immer wieder Leute hierhin verirren, die auf ihre Fragen fast eine Antwort bekommen -- dann aber keinen Kommentar hinterlassen, sondern wortlos wieder abziehen. Wer nach povray mandelbulb sucht, will doch sicher den Code für das Fraktal in einer Form haben, die von PoV-Ray gelesen werden kann? Naja, vielleicht hilft es ja doch noch jemandem, wenn auch der ursprüngliche Besucher längst weg ist (siehe unten).

Außerdem: mein Hauptblog läßt sich wunderbar über Google finden; das Nibelungen-Projekt aber nur über die Blog-Suche. Das finde ich ein bißchen frustrierend, weil es für die Besucherzahlen alles andere als förderlich ist. Naja, vielleicht sollte ich trotzdem noch ein paar Seiten ablichten und vor allem auch transkribieren, damit die Suchmaschinen ein bißchen mehr Text zum Zerkauen haben.

So, das war's auch schon für heute. Ach ja, der Code:

#declare iteratex = function (x, y, z, a) {
a + pow(f_sphere(x,y,z,0),4)*sin(f_ph(y,z,x)*8)
*cos(f_th(y,z,x)*8)}
#declare iteratey = function(x, y, z, b) {
b + pow(f_sphere(x,y,z,0),4)*sin(f_ph(y,z,x)*8)
*sin(f_th(y,z,x)*8)}
#declare iteratez = function(x, y, z, c) {
c + pow(f_sphere(x,y,z,0),4)*cos(f_ph(y,z,x)*8)
}
isosurface {
function {
f_sphere(iteratex(iteratex(iteratex(x,y,z,x), iteratey(x,y,z,y), iteratez(x,y,z,z), x),
iteratey(iteratex(x,y,z,x), iteratey(x,y,z,y), iteratez(x,y,z,z), y),
iteratez(iteratex(x,y,z,x), iteratey(x,y,z,y), iteratez(x,y,z,z), z), x),
iteratey(iteratex(iteratex(x,y,z,x), iteratey(x,y,z,y), iteratez(x,y,z,z), x),
iteratey(iteratex(x,y,z,x), iteratey(x,y,z,y), iteratez(x,y,z,z), y),
iteratez(iteratex(x,y,z,x), iteratey(x,y,z,y), iteratez(x,y,z,z), z), y),
iteratez(iteratex(iteratex(x,y,z,x), iteratey(x,y,z,y), iteratez(x,y,z,z), x),
iteratey(iteratex(x,y,z,x), iteratey(x,y,z,y), iteratez(x,y,z,z), y),
iteratez(iteratex(x,y,z,x), iteratey(x,y,z,y), iteratez(x,y,z,z), z), z), 2)
}
}

[Edit: Typo in den Metadaten]

Das Wort des Tages: Unbill. Außerhalb alter Texte (oder der Fantasy-Literatur) hört man es äußerst selten. Heute aber bat unser IT-Dienstleister, diese zu entschuldigen: ein zentraler Dienst ist vor Weihnachten ausgefallen, der Hersteller arbeitet immer noch an der Behebung des Problems.

Außerdem: Ich habe mich in einem Irrgarten aus Wenn-Dann-Abfragen verlaufen und ein Softwarepaket an zwei Stellen repariert, aber gleichzeitig an drei anderen kaputtgemacht. Bis die Reparatur dann getestet war, ging es schon stark auf acht zu. Naja, wer früh nach Hause will, sollte im Fenster mit den Build-Resultaten vielleicht ganz bis nach rechts scrollen. Dann sähe man nämlich die roten Balken.

Und: Während ich auf den Buildservice warte, bereite ich diesen Blogeintrag in einem TextEdit-Fenster vor. Das Programm mag aber den Satzanfang Naja nicht und ersetzt ihn automatisch durch Anja. Zum Glück kann man das abschalten.

Und zu guter Letzt: Der neue Mandelbulb-Film ist fertig. Es hat ein paar Wochen gedauert, ihn zu berechnen; aber für glatte Kanten und eine höhere Framerate hat ich der Aufwand gelohnt.

Heute gibt es mal wieder ein neues Eckchen (das untere rechte nämlich) in der Reihe des Mandelbulb-Mosaiks. Inzwischen sind die wesentlichen Teile beisammen, und man könnte sich langsam Gedanken über den nächsten Schritt machen, etwa näher heranzugehen. Eine noch höhere Ordnung ist ohne Software-Optimierung wohl nicht sinnvoll.

Diesmal hat es wieder ein bißchen länger gedauert, deshalb gibt es auch ein größeres Stück: die rechte obere Ecke ist fertig -- jedenfalls so weit das Fraktal reich; den Hintergrund reiche ich irgendwann noch nach.

Los ging's übrigens hier, und die ganze Serie findet man per Tag.

Heute habe ich nur eine kleine Briefmarke im oberen Bereich gerechnet, aber dafür ging's auch recht schnell.

Heute ist das Puzzle ein kleines Stückchen weiter.

Vor einiger Zeit hatte ich angekündigt, für ein neues Bild der Mandelbulb eine weitere Iterationsstufe zu berechnen. Leider hat sich PoV-Ray dabei als noch langsamer als befürchtet erwiesen. Damit ich nicht völlig allein meinem Rechner beim Rechnen zusehen muß, gibt es hier eine Vorschau mit drei Iterationsschritten -- nach gut einer Woche kann man schonmal ein bißchen sehen, wie das aussehen wird, wenn es fertig ist. Damit das Bild richtig wirkt, sollte man es sich in groß ansehen.

Zugegeben, ein paar Schritte mehr könnten nicht schaden, die Details auf den Bildern von Daniel White sind (bei zehn Schritten) viel feiner.

Neulich hatte ich mehr zu Mandelbulb, einem dreidimensionalen Fraktal aus der Verwandtschaft des Apfelmännchens versprochen. Jetzt ist -- nach mehreren Tagen Rechenzeit auf einer Zweiprozessormaschine -- endlich der erste Film fertig.

Doch zunächst möchte ich etwas über Folgen erzählen. Folgen sind, nun ja: einfach Aneinanderreihungen von Zahlen; dabei soll das Aneinanderreihen natürlich gewissen Regeln folgen.

Versuchen wir zum Beispiel, eine Zahl immer wieder zu quadrieren: 2, 4, 16, 256, 32768, ...  -- dann bekommen wir ziemlich schnell ziemlich große Zahlen. Das muß aber nicht so sein -- fangen wir doch einfach mit einer kleineren Zahl an, zum Beispiel so: 1, 1, 1, ... -- zugegeben, das ist etwas langweilig: 1²=1, da ist wenig Abwechslung. Vielleicht besser so: 0.1, 0.01, 0.0001, ... -- jetzt wird die Folge sogar immer kleiner. Also: wenn wir auf diese Weise eine Zahl kleiner als Eins fortlaufen quadrieren, so werden die Zahlen immer kleiner; Zahlen größer als Eins werden immer größer, und die Eins selbst bleibt gleich. Daran ändert sich übrigens nicht viel, wenn wir auch negative Anfangswerte zulassen -- das Minuszeichen fällt im ersten Schritt weg, und dann geht es weiter wie bekannt. Wenn wir uns also den Zahlenstrahl aus der Schule aufmalen, dann könnte das etwa so aussehen:

Alles, was zwischen -1 und +1 liegt, bleibt endlich; alle anderen Zahlen werden durch das Quadrieren immer größer. Wir könnten jetzt unsere Rechenvorschrift (das Quadrieren) komplizierter machen, aber lustige Bilder werden wir auf diese Weise nicht erhalten: der Zahlenstrahl ist ja nur eine einzige Linie, was kann man daraus schon groß machen? Schöner wäre es, wenn wir eine Fläche hätten, etwa so:

Nur: wie verteilen wir unsere Zahlen darauf? Das ist in der Mathematik zum Glück kein Problem: wir denken uns einfach neue Zahlen aus, so daß wir nicht nur links von der Eins die Null und rechts die Zwei haben, sondern auch über und unter der Eins noch Zahlen hinschreiben können. Jetzt müssen wir nur noch überlegen, wie wir diese Zahlen quadrieren können, und das machen wir so:

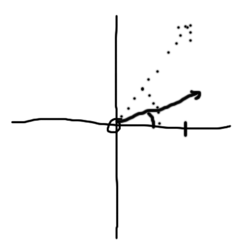Wir denken unz zu jeder Zahl eine Art Uhrzeiger. Wenn wir die Zahl quadrieren wollen, dann quadrieren wir zuerst einfach seine Länge. Außerdem drehen wir den Zeiger ein Stück weiter: aus ein Uhr wird zwei Uhr, aus drei Uhr wird sechs Uhr, und aus vier Uhr wird acht Uhr. Bevor jetzt jemand fragt: bei den Mathematikern gehen die Uhren linksherum; und in diesem speziellen Fall fängt man auch gerne rechts statt oben an mit null Uhr.

Diese Definition mag ein bißchen seltsam wirken, aber sie hat einen großen Vorteil: wenn wir uns Zahlen auf dem guten alten Zahlenstrahl ansehen, dann liegen die ja auf null Uhr (die positiven) oder auf sechs Uhr (die negativen); und wenn wir die jetzt nach der neuen Regel quadrieren, dann drehen wir die positiven gar nicht (sie stehen ja, wie gesagt, auf null Uhr), und die negativen von sechs auf zwölf Uhr -- oder eben wieder null. Also: nach dem Quadrieren landen alle Zahlen vom Zahlenstrahl wieder auf der positiven Hälfte des Strahls, und weil wir ja die Zeigerlängen außerdem quadrieren, erhalten wir das selbe Ergebnis wie bei der Rechnung nach Schulregeln.

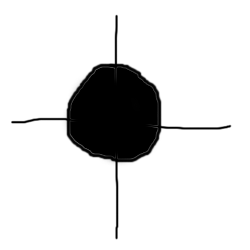Jetzt gehen wir nochmals zu den Folgen zurück und quadrieren munter drauflos. Das Ergebnis ist recht einleuchtend: unsere Zeigerzahlen drehen sich wild im Kreis, aber alle Zeiger länger als Eins wachsen ins unermeßliche, während die kürzeren ins Nichts schrumpfen.

Damit haben wir immerhin ein kleines Bild, wenn auch kein besonders aufregendes: einen Kreis mit dem Radius eins nämlich, der alle die Zahlen bezeichnet, die beim Quadrieren immer weiter schrumpfen.

Es mag einleuchten, daß man mit einer komplizierteren Rechenvorschrift auch komplexere Bilder erzeugen kann. Wer jetzt aber glaubt, daß man eine die Regel sehr viel komplizierter machen muß, der hat sich getäuscht: wie wäre es zum Beispiel, wenn wir unsere Zahl immer abwechselnd quadrieren und addieren? Das ginge dann so: 1²=1, 1+1=2, 2²=4, 4+1=5, 5²=25; also: 1, 2, 4, 5, 25, ... und die Zahlen werden immer größer. Bei den negativen gibt es aber eine kleine Überraschung: -2²=4, 4+(-2)=2, 2²=4, 4+(-2)=2... hier kommen wir über die Zwei nicht hinaus! Wir werden also, wenn wir wieder alle konvergenten Folgen (also die, die endlich bleiben) schwarz anmalen, keinen Kreis erhalten: die +1 müßte ja weiß bleiben, die -2 hingegen wäre schwarz. Ein Oval vielleicht? Es ist auf Anhieb nicht klar, was mit unseren Uhrenzahlen[1] passieren würde, und so hilft es nur, den Computer zuhilfe zu nehmen und das Bild auszurechnen -- und dann passiert das:

Ich finde es überraschend und sehr erstaunlich, daß aus einer so einfachen Formel ein so komplexes Gebilde entsteht, und gerade diese Einfachheit macht für mich einen Großteil der Schönheit des Apfelmännchens aus: bekommt man doch soviel mehr heraus, als man hineingesteckt hat.

Zu guter Letzt möchte ich noch meinen Film von der dreidimensionalen Variante zeigen. Wie man hier rechnet, erkläre ich aber erst im nächsten Blogeintrag. Wenn das Fraktal hier recht glatt erscheint (während doch das zweidimensionale Apfelmännchen arg pieksig wirkt), so liegt das nicht in der Natur der Sache; vielmehr habe ich, um überhaupt in sinnvoller Zeit zu einem Ergebnis zu kommen, nur die ersten zwei Schritte der Folgen berechnet. Um ein realistischeres Bild zu erhalten, hätte ich zehn Schritte rechnen müssen. Und an der pixeligen Struktur arbeite ich auch noch...

[1]Der aufmerksame Leser mag bemerken, daß wir oben zwar das Quadrieren, nicht aber die Addition der Uhrenzahlen definiert haben. Letztere ist aber recht einfach: um zwei Zeiger zu addieren, verschieben wir einen von ihnen so, daß sein Fußpunkt an der Spitze des anderen zu liegen kommt; seine Richtung soll er dabei nicht verändern. Die Summe der beiden ist dann ein neuer Zeiger, der vom Fußpunkt des unverschobenen zur Spitze des verschobenen Zeigers geht. Wer mit dem Konzept der Vektorrechnung vertraut ist, wird hier die Vektoraddition erkennen[2].

[2]Und wer mit dem Konzept der komplexen Zahlen vertraut ist, wird diese in unseren Uhrenzahlen erkennen.

Anfang dieser Woche erschien auf Slashdot die Nachricht, daß ein dreidimensionales Äquivalent zur Mandelbrot-Menge, auch bekannt als Apfelmännchen, gefunden wurde. Ein Blick auf die Seite von Daniel White offenbarte nicht nur eine Erklärung, sondern auch atemberaubende Bilder -- und in mir erwachte sogleich der Wunsch, mich selbst daran zu versuchen.

Gebrochen

Die Klasse der Objekte, zu der das Apfelmännchen genauso wie der neue Mandelbulb gehören, nennt man Fraktale. Was bedeutet das eigentlich? Nun, in der Mathematik versteht man unter einem Fraktal ein Gebilde, dessen Dimension keine ganze Zahl ist. Es ist zunächst schwer vorstellbar, was das bedeuten soll: entweder habe ich etwas eindimensionales, etwa eine Linie; oder ein Blatt Papier, das (wenn wir seine Dicke einmal ignorieren) zweidimensional ist; oder aber zum Beispiel einen Würfel. Der hat drei Dimensionen -- aber zweieinhalb?

Wenn wir uns die Dimension eines Vektorraumes ansehen, ist das in der Tat nicht möglich: vereinfacht gesagt, zählt man schlicht die (voneinander unabhängigen) Richtungen, die es in einem Objekt gibt, und nennt diese die Dimension: wenn es nur Länge gibt (zum Beispiel bei einem Bindfaden), dann ist die Dimension Eins. Das Wohnzimmer hat Länge, Breite und Höhe, also die Dimension Drei.

Ich kann aber auch anders vorgehen: dazu nehme ich mir einen Ball, der groß genug ist, um den Bindfaden darunter zu verstecken. Ist der Faden z.B. einen Meter lang, dann brauche ich einen Ball, der einen Meter Durchmesser hat. Nun probiere ich es mit einem Ball von einem halben Meter -- und stelle fest, daß ich zwei davon brauche, um den Faden abzudecken. Hat mein Ball nur 10 cm Durchmesser (ein Zehntel des ursprünglichen), dann brauche ich auch zehn Bälle, und so weiter.

In meinem Wohnzimmer geht das nicht: während ich das komplette Zimmer in einen Ball mit fünf Metern Durchmesser stecken könnte, benötige ich wesentlich mehr als fünf Bälle, wenn diese nur einen Meter Durchmesser haben, nämlich mehr als hundert. Die Dimension eines Objekts sagt mir also, wie schnell die Zahl der nötigen Bälle wächst, wenn ich die Bälle selbst kleiner mache. Bei einem eindimensionalen Gegenstand reichen 2 Bälle der Größe 1/2, bei einem dreidimensionalen brauche ich 8, das sind 2³.

Jetzt drehen wir den Spieß um und erheben diese Ballzählerei zur Definition: das Schachbrett ist deshalb zweidimensional, weil ich 64=8² Felder der Größe 1/8 brauche, um es abzudecken.

Radieren

Wie muß nun ein Objekt aussehen, damit ich bei dieser Rechnung krumme Zahlen erhalte? Dazu wollen wir ein kleines Experiment machen. Dazu benötigen wir nur ein Blatt Papier, einen Bleistift, ein Radiergummi, und vielleicht noch ein Lineal. Zunächst zeichnen wir eine gerade Linie auf das Blatt, etwa so:

Nun nehmen wir das Radiergummi und entfernen das mittlere Drittel der Linie:

Von den beiden kürzeren Linien, die nun übrig bleiben, entfernen wir jeweils wieder das mittlere Drittel:

Und so weiter -- im Prinzip geht das beliebig lange, wenn nur unser Radiergummi fein genug ist:

Was passiert, wenn wir dieses Gebilde mit Bällen zudecken wollen? Nun, fangen wir mit einem Ball an, der gerade groß genug ist, um alle Teilstücke der Linie zu überdecken. Wenn wir diesen Ball dritteln, dann brauchen wir aber mitnichten drei der kleineren Bälle -- es genügen zweie, einer für die linke Seite, einer für die rechte. In der Mitte haben wir ja alles wegradiert. Wenn wir also einen Ball der Größe 1/3 wählen, brauchen wir 2=3^0.63 Exemplare davon. Deshalb können wir sagen, daß unser Kunstwerk die Dimension 0.63 hat. Genauer betrachtet, ist das auch gar nicht so abwegig: wir haben da eine Unmenge von Punkten, die sehr dicht beieinander liegen. Einzelne Punkte hätten die Dimension 0; und wenn sie unendlich dicht beieinander lägen, hätten wir eine Linie mit der Dimension 1. Daß unser Ergebnis irgendwo dazwischen liegt, ist nicht so verwunderlich.

Ganz ähnlich verhält es sich auch beim Apfelmännchen: egal, wie stark ich Ausschnitte davon vergrößere, es gibt immer feinere Strukturen zu entdecken. Das trifft im Prinzip auch auf die oben abgebildete Mandelbulb zu; allerdings ist die Abbildung mit einer sehr vereinfachten Formel erstellt worden, weshalb nur die gröbsten Knubbel zu erkennen sind -- ganz so, als ob ich beim Zerteilen der Linie nach zweimaligem Radieren aufhöre.

Demnächst in diesem Theater

In den kommenden Tagen möchte ich noch kurz anreißen, wie man das Apfelmännchen und die Mandelbulb berechnet; außerdem gibt es dann hoffentlich mehr Bilder und vielleicht sogar Filme zu sehen.

[Edit: Typos]