NOV
2009
Neulich hatte ich mehr zu Mandelbulb, einem dreidimensionalen Fraktal aus der Verwandtschaft des Apfelmännchens versprochen. Jetzt ist -- nach mehreren Tagen Rechenzeit auf einer Zweiprozessormaschine -- endlich der erste Film fertig.
Doch zunächst möchte ich etwas über Folgen erzählen. Folgen sind, nun ja: einfach Aneinanderreihungen von Zahlen; dabei soll das Aneinanderreihen natürlich gewissen Regeln folgen.
Versuchen wir zum Beispiel, eine Zahl immer wieder zu quadrieren: 2, 4, 16, 256, 32768, ... -- dann bekommen wir ziemlich schnell ziemlich große Zahlen. Das muß aber nicht so sein -- fangen wir doch einfach mit einer kleineren Zahl an, zum Beispiel so: 1, 1, 1, ... -- zugegeben, das ist etwas langweilig: 12=1, da ist wenig Abwechslung. Vielleicht besser so: 0.1, 0.01, 0.0001, ... -- jetzt wird die Folge sogar immer kleiner. Also: wenn wir auf diese Weise eine Zahl kleiner als Eins fortlaufen quadrieren, so werden die Zahlen immer kleiner; Zahlen größer als Eins werden immer größer, und die Eins selbst bleibt gleich. Daran ändert sich übrigens nicht viel, wenn wir auch negative Anfangswerte zulassen -- das Minuszeichen fällt im ersten Schritt weg, und dann geht es weiter wie bekannt. Wenn wir uns also den Zahlenstrahl aus der Schule aufmalen, dann könnte das etwa so aussehen:

Alles, was zwischen -1 und +1 liegt, bleibt endlich; alle anderen Zahlen werden durch das Quadrieren immer größer. Wir könnten jetzt unsere Rechenvorschrift (das Quadrieren) komplizierter machen, aber lustige Bilder werden wir auf diese Weise nicht erhalten: der Zahlenstrahl ist ja nur eine einzige Linie, was kann man daraus schon groß machen? Schöner wäre es, wenn wir eine Fläche hätten, etwa so:
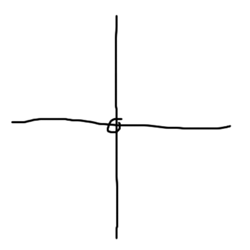
Nur: wie verteilen wir unsere Zahlen darauf? Das ist in der Mathematik zum Glück kein Problem: wir denken uns einfach neue Zahlen aus, so daß wir nicht nur links von der Eins die Null und rechts die Zwei haben, sondern auch über und unter der Eins noch Zahlen hinschreiben können. Jetzt müssen wir nur noch überlegen, wie wir diese Zahlen quadrieren können, und das machen wir so:
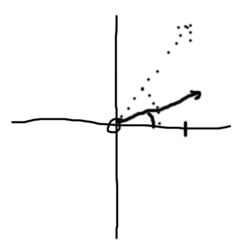 Wir denken unz zu jeder Zahl eine Art Uhrzeiger. Wenn wir die Zahl quadrieren wollen, dann quadrieren wir zuerst einfach seine Länge. Außerdem drehen wir den Zeiger ein Stück weiter: aus ein Uhr wird zwei Uhr, aus drei Uhr wird sechs Uhr, und aus vier Uhr wird acht Uhr. Bevor jetzt jemand fragt: bei den Mathematikern gehen die Uhren linksherum; und in diesem speziellen Fall fängt man auch gerne rechts statt oben an mit null Uhr.
Wir denken unz zu jeder Zahl eine Art Uhrzeiger. Wenn wir die Zahl quadrieren wollen, dann quadrieren wir zuerst einfach seine Länge. Außerdem drehen wir den Zeiger ein Stück weiter: aus ein Uhr wird zwei Uhr, aus drei Uhr wird sechs Uhr, und aus vier Uhr wird acht Uhr. Bevor jetzt jemand fragt: bei den Mathematikern gehen die Uhren linksherum; und in diesem speziellen Fall fängt man auch gerne rechts statt oben an mit null Uhr.
Diese Definition mag ein bißchen seltsam wirken, aber sie hat einen großen Vorteil: wenn wir uns Zahlen auf dem guten alten Zahlenstrahl ansehen, dann liegen die ja auf null Uhr (die positiven) oder auf sechs Uhr (die negativen); und wenn wir die jetzt nach der neuen Regel quadrieren, dann drehen wir die positiven gar nicht (sie stehen ja, wie gesagt, auf null Uhr), und die negativen von sechs auf zwölf Uhr -- oder eben wieder null. Also: nach dem Quadrieren landen alle Zahlen vom Zahlenstrahl wieder auf der positiven Hälfte des Strahls, und weil wir ja die Zeigerlängen außerdem quadrieren, erhalten wir das selbe Ergebnis wie bei der Rechnung nach Schulregeln.
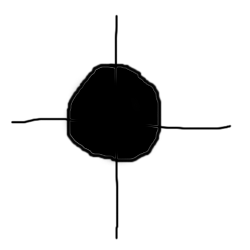 Jetzt gehen wir nochmals zu den Folgen zurück und quadrieren munter drauflos. Das Ergebnis ist recht einleuchtend: unsere Zeigerzahlen drehen sich wild im Kreis, aber alle Zeiger länger als Eins wachsen ins unermeßliche, während die kürzeren ins Nichts schrumpfen.
Jetzt gehen wir nochmals zu den Folgen zurück und quadrieren munter drauflos. Das Ergebnis ist recht einleuchtend: unsere Zeigerzahlen drehen sich wild im Kreis, aber alle Zeiger länger als Eins wachsen ins unermeßliche, während die kürzeren ins Nichts schrumpfen.
Damit haben wir immerhin ein kleines Bild, wenn auch kein besonders aufregendes: einen Kreis mit dem Radius eins nämlich, der alle die Zahlen bezeichnet, die beim Quadrieren immer weiter schrumpfen.
Es mag einleuchten, daß man mit einer komplizierteren Rechenvorschrift auch komplexere Bilder erzeugen kann. Wer jetzt aber glaubt, daß man eine die Regel sehr viel komplizierter machen muß, der hat sich getäuscht: wie wäre es zum Beispiel, wenn wir unsere Zahl immer abwechselnd quadrieren und addieren? Das ginge dann so: 12=1, 1+1=2, 22=4, 4+1=5, 52=25; also: 1, 2, 4, 5, 25, ... und die Zahlen werden immer größer. Bei den negativen gibt es aber eine kleine Überraschung: -22=4, 4+(-2)=2, 22=4, 4+(-2)=2... hier kommen wir über die Zwei nicht hinaus! Wir werden also, wenn wir wieder alle konvergenten Folgen (also die, die endlich bleiben) schwarz anmalen, keinen Kreis erhalten: die +1 müßte ja weiß bleiben, die -2 hingegen wäre schwarz. Ein Oval vielleicht? Es ist auf Anhieb nicht klar, was mit unseren Uhrenzahlen[1] passieren würde, und so hilft es nur, den Computer zuhilfe zu nehmen und das Bild auszurechnen -- und dann passiert das:

Ich finde es überraschend und sehr erstaunlich, daß aus einer so einfachen Formel ein so komplexes Gebilde entsteht, und gerade diese Einfachheit macht für mich einen Großteil der Schönheit des Apfelmännchens aus: bekommt man doch soviel mehr heraus, als man hineingesteckt hat.
Zu guter Letzt möchte ich noch meinen Film von der dreidimensionalen Variante zeigen. Wie man hier rechnet, erkläre ich aber erst im nächsten Blogeintrag. Wenn das Fraktal hier recht glatt erscheint (während doch das zweidimensionale Apfelmännchen arg pieksig wirkt), so liegt das nicht in der Natur der Sache; vielmehr habe ich, um überhaupt in sinnvoller Zeit zu einem Ergebnis zu kommen, nur die ersten zwei Schritte der Folgen berechnet. Um ein realistischeres Bild zu erhalten, hätte ich zehn Schritte rechnen müssen. Und an der pixeligen Struktur arbeite ich auch noch...
[1]Der aufmerksame Leser mag bemerken, daß wir oben zwar das Quadrieren, nicht aber die Addition der Uhrenzahlen definiert haben. Letztere ist aber recht einfach: um zwei Zeiger zu addieren, verschieben wir einen von ihnen so, daß sein Fußpunkt an der Spitze des anderen zu liegen kommt; seine Richtung soll er dabei nicht verändern. Die Summe der beiden ist dann ein neuer Zeiger, der vom Fußpunkt des unverschobenen zur Spitze des verschobenen Zeigers geht. Wer mit dem Konzept der Vektorrechnung vertraut ist, wird hier die Vektoraddition erkennen[2].
[2]Und wer mit dem Konzept der komplexen Zahlen vertraut ist, wird diese in unseren Uhrenzahlen erkennen.
1 Kommentar • english