kirjoittaessani

Es wird Zeit, sich noch einmal mit Landkarten zu beschäftigen. Wir haben bereits gesehen, daß ein Tuschekasten für Kartographen mindestens vier Farben enthalten muß. Außerdem braucht man dann, wenn für jedes Land eine Liste von Farben gebildet werden soll, höchstens mehr, niemals aber weniger Farben.
Noch offen ist aber die Frage, ob ich einen Tuschekasten zusammenstellen kann, mit dem jeder Kartograph für alle Karten auskommt.

Behauptung

Ich behaupte: ja, das geht. Fünf Farben reichen aus.
Mehr noch: es genügt sogar, wenn für jedes Land eine Liste mit fünf Farben zur Verfügung steht. (Wir hatten ja gesehen, daß das ein schwierigeres Problem ist.)

Induziert

Wie beweist man das am besten? Das Verfahren der vollständigen Induktion bietet sich hier an: Eine Karte mit nicht mehr als fünf Ländern kann ich natürlich immer mit fünf Farben zeichnen (Induktionsanfang). Wenn ich jetzt aus einer Karte mit n Ländern auf geschickte Weise ein Land eliminieren könnte, wäre ich schon am Ziel. Aber wie stellt man das an?
Als erstes greifen wir tief in die Trickkiste und fördern etwas zutage, das sich Warum einfach, wenn's auch kompliziert geht? nennt: wir beweisen schlichtweg etwas, das schwieriger (stärker) ist, und machen uns die Arbeit dadurch einfacher. Das hört sich seltsam an; der Grund liegt aber darin, daß wir uns sozusagen auf der Leiter von Sprosse zu Sprosse hangeln. Wenn wir alle Sprossen etwas höher einbauen, müssen wir zwar mit jedem Schritt etwas höher hinauf als bei unserer Originalleiter, aber wir starten ja auch jeden Schritt von einer höheren Sprosse aus.

Wirklich schwieriger wird nur die erste Sprosse; die ist aber bei Induktionsbeweisen kein wirkliches Problem. Zugegeben, ein bißchen hinkt die Analogie schon: wenn ich die Behauptung stärker mache, so kann der Beweis tatsächlich gleich schwer bleiben (wie bei der Leiter), er kann aber auch schwieriger oder einfacher werden. Hier wird er erfreulicherweise einfacher.

Weiter im Text

Weiter wollen wir annehmen, daß es höchstens Drei-Länder-Ecke gibt — aber keine Vier-, Fünf-, oder Noch-mehr-Länder-Ecke.

Wenn wir es doch einmal mit einer solchen Karte zu tun haben sollten, wollen wir einfach die Grenzen ein bißchen verschieben. Das ist nicht schlimm, weil das Problem dadurch nur schwieriger wird, die neue Lösung also auf jeden Fall auch Lösung des ursprünglichen Problems ist.

Behaupten kann man viel

Sehen wir uns eine Karte an, dann gibt es dort immer einen Ring von äußeren Ländern; hier sind es z.B. Washington, Oregon, Kalifornien, Arizona, New Mexico, Texas und so weiter.

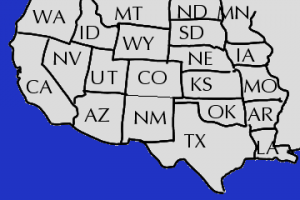
Seien nun zwei benachbarte Länder dieses Rings bereits eingefärbt; jedes weitere Land auf dem Ring stelle eine Liste mit (mindestens) drei Farben bereit; jedes Land aus dem Inneren stelle eine Liste mit mindestens fünf Farben bereit.
Dann — so unsere Behauptung — können wir die gesamte Karte unter Benutzung dieser Listen einfärben.

Stärke

Diese Behauptung hat mit unserem ursprünglichen Ziel — der Einfärbung der Karte unter Benutzung von Fünfer-Farblisten — nicht mehr viel zu tun. Sie ist aber stärker: Wir behaupten jetzt, daß nur die inneren Länder noch Fünfer-Listen bereitstellen sollen; die Länder auf dem Ring liefern nur noch Dreier-Listen, zwei geben ihre Farbe sogar fest vor. Wenn wir die Karte unter diesen Bedingungen färben können, kommen wir mit Fünfer-Listen auf jeden Fall hin.

Aller Anfang ist leicht

Wenn nur drei Länder auf der Karte sind, so reichen uns die Farben auf jeden Fall: zweie sind ja schon gefärbt, und das dritte bietet uns eine Liste mit drei Farben an; egal, welche Farben durch die beiden Nachbarn belegt sind, eine bleibt immer frei.

Ein kleiner Schritt für einen Kartographen

Erinnern wir uns an die Vorgehensweise beim Induktionsschritt: wir müssen die Behauptung für eine Karte mit n Ländern beweisen, dürfen aber annehmen, sie sei für n-1 Länder, ja sogar für alle möglichen Karten mit weniger als n Ländern bereits bewiesen. Wir müssen also unsere große Karte auf eine (oder zwei) kleinere Karten zurückführen.
Nehmen wir nun an, zwei Länder aus dem äußeren Ring haben eine gemeinsame Grenze, die aber selbst nicht nach außen stößt; der Ring hat dann die Form einer Acht. Zaire und der Sudan sind ein Beispiel.

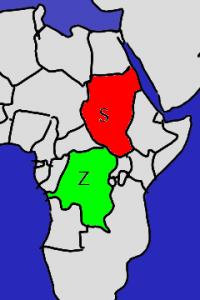
Jetzt können wir die Karte in zwei Teile zerlegen: die eine enthält Zaire, den Sudan, und alle weiter nördlich gelegenen Länder; die andere enthält ebenfalls Zaire und den Sudan, dazu aber die südlicheren Länder. Für Zaire und den Sudan vergeben wir jetzt je eine Farbe fest (etwa grün und rot); alle anderen Länder auf dem alten Ring haben Listen mit drei Farben, die inneren Länder deren fünf — so war ja die Voraussetzung. Dann gilt das aber auch für jede der beiden neuen "halben" Karten. Da diese kleiner sind, dürfen wir die Behauptung als bereits bewiesen ansehen. Beide kleinen Karten sind also mit den vorgegebenen Farben einfärbbar, und damit auch die gesamte Karte.
Das war es auch schon — mehr hatten wir gar nicht behauptet.

Unachtsam

Was nun, wenn der äußere Ring nicht die Form einer Acht hat?
Dann müssen wir die Zahl der Länder eben auf andere Art verringern. Nehmen wir die Karte der USA von oben, dann hat der äußere Ring dort nicht die Form einer Acht.

Angenommen, Washington sei bereits blau gefärbt. Auf dem Ring hat dieser Staat zwei Nachbarn: Idaho und Kalifornien. Angenommen, Idaho sei ebenfalls gefärbt (nach Annahme muß es ein Nachbar Washingtons auf dem Ring sein; es bleiben also nur CA oder ID). Dann entfernen wir jetzt probehalber Kalifornien von der Karte. Dadurch wird Nevada neu in den äußeren Ring aufgenommen — bei einer anderen Karte könnte natürlich auch eine ganze Reihe von Staaten dazukommen.
Nach Annahme hat Kalifornien (mindestens) eine Liste von drei Farben zur Verfügung gestellt; davon müssen mindestens zwei von Blau verschieden sein (sagen wir, Rot und Gelb). Diese beiden Farben streichen wir jetzt von der Farbliste Nevadas. Da die Liste vorher mindestens fünf Farben enthielt, bleiben also jetzt noch drei. Das heißt aber, daß die neue Karte (ohne Kalifornien) alle Voraussetzungen erfüllt, um vorschriftsmäßig gefärbt zu werden. Wenn wir jetzt noch eine Farbe für Kalifornien finden, sind wir fertig. Das ist aber leicht:
Nevada kann weder rot noch gelb sein, da wir diese Farben von der Liste gestrichen haben. Washington ist schon blau, und Arizona kann entweder Rot oder Gelb (oder eine andere Farbe) erhalten, aber nicht beide; deswegen bleibt eine der beiden Farben Rot und Gelb für Kalifornien.

Das war's, die Karte ist gefärbt!

Und sonst?

Im Falle der Farblisten ist Fünf tatsächlich die kleinste Zahl, die man finden kann. Margit Voigt hat ein Beispiel gefunden für eine Karte, die sich mit Vierer-Farblisten nicht immer einfärben läßt. Sie hat 238 Länder eingezeichnet.

Wenn es nur um den Tuschekasten geht, reichen dagegen sogar vier Farben. Der Beweis dafür ist allerdings leider viel zu lang und kompliziert für dieses Blog.

Der obige Beweis folgt übrigens dem Buch von Martin Aigner und Günther Ziegler, in dem sich — etwa auf Vordiplomniveau — eine ganze Reihe schöner Beweise findet.

Im Moment ist Orangenzeit, und da dachte ich mir, daß ich eigentlich mal wieder Marmelade kochen könnte.
Also habe ich mir schnell ein Rezept ergoogled, zwei Kilo Orangen und zwei Packungen Zucker gekauft, und los geht's.

Die richtigen Seville Oranges aus dem Rezept habe ich natürlich nicht gefunden, aber normale tun es hoffentlich auch. Zur Ergänzung kommen noch zwei Zitronen dazu.

Nun gut, also alles kleinschneiden und ab in den Kühlschrank damit.

Am nächsten Tag steht dann die Kochorgie an. Schwierig wird es am Ende:
With experience one learns to recognize the developments, in terms of the appearance of the jam and the slightly sticky sound of the bubbling
Sticky sound? Keine Ahnung. Ich schaufele also fleißig Teelöffel auf Teelöffel aus dem Topf, aber irgendwie bleibt das Zeug unverändert flüssig.

Irgendwann verliere ich die Geduld dräut der Invertzucker zu sehr, und ich schaufele die Masse so, wie sie ist, in die Gläser.

Ergebnis: der Geschmack ist durchaus OK, aber eine flüssigere Marmelade habe ich noch nie gesehen.

Der Spiegel berichtet — nicht zum ersten Mal — über einen Bochumer Mathematiker, der die deutschen Zahlwörter ändern will: Einundzwanzig sei unlogisch, er möchte deshalb zwanzigeins einführen.
Der Artikel liest sich stellenweise, als ob der Untergang des Abendlandes oder doch wenigstens ein schlechtes Abschneiden bei der PISA-Studie drohte, wenn diese Änderung nicht durchgeführt wird. Ich habe da ein ganz anderes Problem: wo haben sie in dem Artikel nur die Smilies versteckt?

Frühling!

Heute hat hier jemand falsche mathematische beweise lustige gesucht. Über die Wortstellung sehe ich ja großzügig hinweg, aber falsche Beweise?
Hier gibt es natürlich nur richtige Beweise. Diese Impertinenz!

Bei Spon können wir heute lernen, daß Kaffee ja eigentlich doch ein fürchterlich gesundes Getränk ist. Gleichzeitig stellt sich aber die Frage, ob eine gründliche Beherrschung der deutschen Sprache heutzutage für einen Journalisten nicht mehr nötig ist, oder ob sich der Redaktionskaffee vielleicht doch negativ ausgewirkt hat.
Auch diese Meinungsfeste wird geschliffen
Abgesehen von der fürchterlichen Metapher ist es natürlich schön, wenn die Formulierungen geschliffen sind, aber die Feste? Womit eigentlich — Papier? Das paßt ja zum Beruf des Journalisten, aber welche Körnung mag er verwenden? Vielleicht sähe er es doch lieber, die Feste würde geschleift?
Fragen über Fragen.

Bei Telepolis schreibt Gerhard Fröhlich über Unethische Autorenschaften; also Wissenschaftler, die als Autoren bei einem Beitrag aufgeführt sind, obwohl sie nicht an seiner Entstehung mitgearbeitet haben, oder umgekehrt Autoren, deren Namen nicht genannt werden.

Der Katalog der Verfehlungen liest sich teils ziemlich greulich, aber wer jetzt den Eindruck bekommt, daß grundsätzlich alle Autorenlisten frisiert sind, der irrt glücklicherweise.

Ich kenne durchaus Institutsleiter, die nur dann in der Autorenliste erscheinen, wenn sie auch tatsächlich am Paper mitgearbeitet haben; und wenn bei uns jemandem für helpful comments gedankt wird, dann hat er auch genau diese beigetragen — in der Regel im Rahmen der weiter unten im Artikel erwähnten Kaffeepausen-Gespräche.
Wer wirklich substanziell mitgearbeitet hat, wird selbstverständlich auch Koautor.

Und was das Pingpong der "kühnen Vermutungen" (Popper), Scherze, Einwände und Gegenkritiken anbetrifft, so bleibt doch anzumerken, daß es — zumindest in den Naturwissenschaften — damit nicht getan ist. Von dem Augenblick, in dem die Idee und die Überzeugung ja, so könnte es gehen da sind, bis zu dem Moment, da alle Daten für eine Veröffentlichung stehen, ist es eben ein langer und arbeitsreicher Weg.

In letzter Zeit lese ich im Kaufhaus immer öfter Sätze der Art:
WeihnachtsOsterdekoration finden Sie auf unserer Sonderfläche im 2. Stock. Was für ein Wort. Es klingt nach einem Marketing-Fachbegriff, der nur versehentlich auf einem für Kunden sichtbaren Plakat gelandet ist.

Als alter Fan von Crosby, Stills, Nash & Young im Trio oder Quartett kann ich auch an Soloalben der vier nur selten vorbeigehen.
Ganz besonders gilt das für Stephen Stills, dessen Stimme mir von den vieren am besten gefällt, auch wenn Graf und Rausch ihn bloß als passablen Sänger bezeichnen.
Zugegeben, im Chor mit den anderen klingt das dann noch viel besser.

Als ich neulich über Stills' Debutalbum gestolpert bin, habe ich es natürlich sofort mitgenommen — trotz des frostigen Covers.
Das erste Stück ist gleich auch das bekannteste, nämlich Love the one you're with. Ich bin mir noch nicht ganz sicher, ob es wirklich das beste ist, es hat jedenfalls den deutlichsten Hit-Charakter. Die meisten Titel sind aber wesentlich ruhiger als der Auftakt. To a flame ist einer davon, ziemlich melancholisch, aber mit Vibraphon, einem Instrument, das auf meiner persönlichen Favoritenliste ziemlich weit oben steht.

Black queen dagegen besteht nur aus Gitarre und Gesang und ist so sehr southern, daß vor meinem geistigen Auge direkt ein Whiskey-Werbespot entsteht. Gesponsert hat den Live-Auftritt aber Jose Cuervo Tequila.
Außer Stills selbst ist noch eine ordentliche Ansammlung bekannter Musiker zu hören, unter anderen Rita Coolidge, Priscilla Jones, John Sebastian sowie Crosby & Nash als Sänger. Bei Old times good times spielt Jimi Hendrix Gitarre, bei Go back home Eric Clapton.

Und im Ganzen? Eher was für spätabends als tagsüber; und: es zieht mich immer wieder zu Love the one you're with.